החבורה הדיהדרלית

פעם אחת, לפני שנים רבות רבות, לפני שעוד היו לפטופים ואולי בכלל לפני המצאת המחשב, נהגו להשתמש במשהו מוזר שנקרא “שקפים” כדי להראות מצגות. שקף, כשמו כן הוא, היה דף שעשוי מחומר שקוף שהאור עובר דרכו. על השקף היו כותבים או מדפיסים טקסט, תמונות וכדומה, ואז שמים אותו על “מקרן” שהיה מעביר דרכו אור ואז באמצעות מראה משגר את האור הזה לעבר מסך, והתמונה על המסך הייתה תואמת את התמונה שמופיעה בשקף. ולמה אני מספר לכם על המוצג ההיסטורי הזה? כי אני רוצה שתדמיינו שבאים אליכם עכשיו שקף כזה עם איזו תמונה נחמדה עליו, שמים אותו על שולחן גדול, ואז אומרים לכם להזיז את השקף הזה איך שבא לכם. אני יושב בצד ומצלם את מה שאתם עושים עם השקף, ובסוף אנחנו יושבים לראות את ההקלטה ומנסים להבין את סוג הפעולות שביצעתם עם השקף. אילו דברים אנחנו עשויים לראות?

ובכן, אתם עשויים להזיז את השקף ימינה/שמאלה. אתם גם עשויים להזיז אותו קדימה/אחורה על השולחן (אפשר גם לקרוא לזה “למעלה/למטה”, תלוי מאיזו זווית אתם מסתכלים על השולחן). אתם גם יכולים לעשות הזזה מורכבת יותר, אבל אפשר יהיה לחשוב עליה כאילו ביצעתם הזזה ימינה/שמאלה ואז ביצעתם הזזה קדימה/אחורה: ההזזה המורכבת היא, ובכן, הרכבה של שתי ההזזות הפשוטות יותר.

עוד דבר שאתם יכולים לעשות הוא לסובב את השקף. מה זה סיבוב? בוחרים נקודה כלשהי על השולחן שהיא הציר שלנו, ומסובבים את הכל סביבה. אפשר לסובב בכל זווית שהיא בין 0 ל-360 מעלות. אפשר כמובן גם לשלב בין סיבוב ובין הזזה.

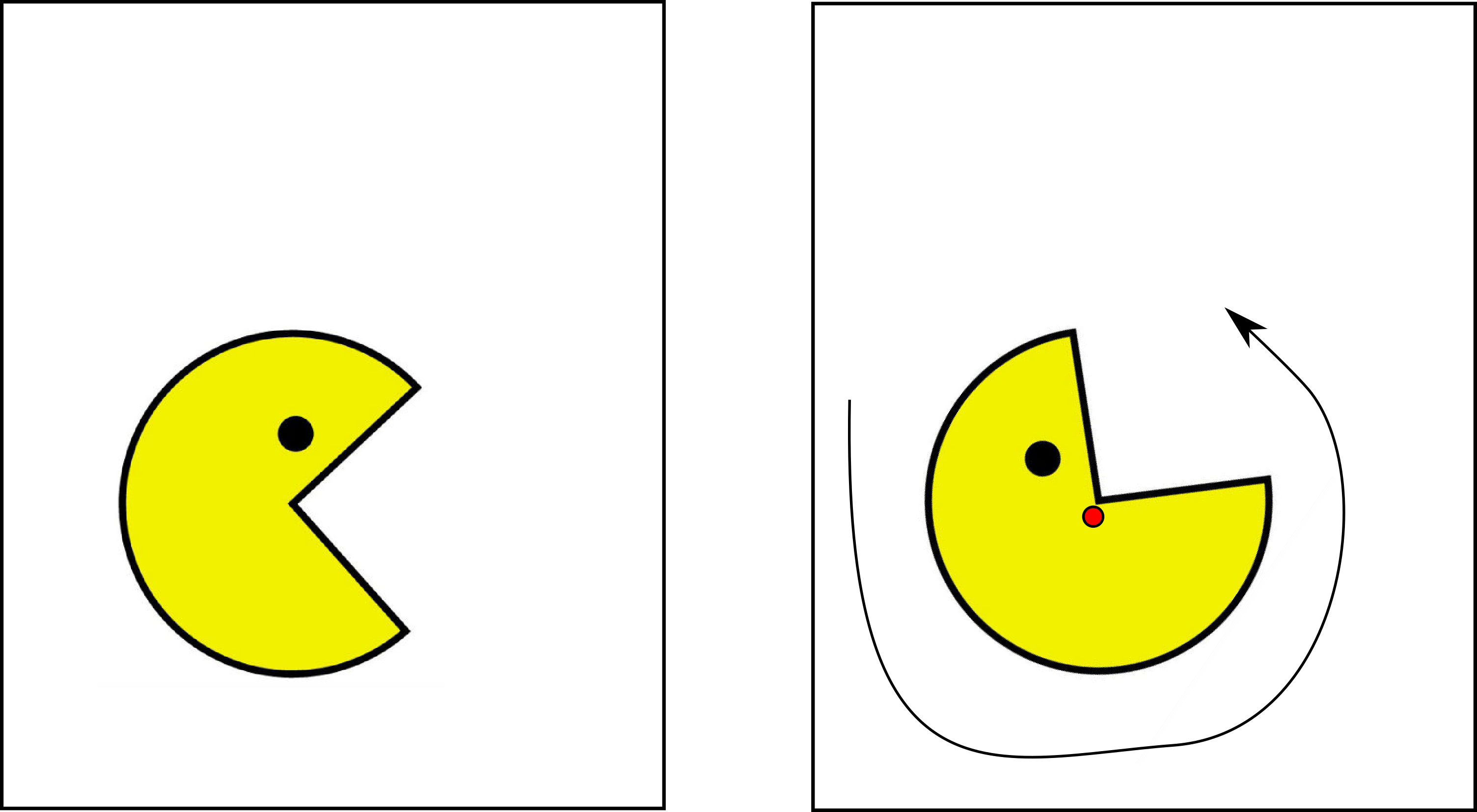
ויש עוד דבר שאפשר לעשות, ונזהרתי לא לנסח את חוקי המשחק בצורה שתאסור אותו אבל גם לא תגיד אותו במפורש: אפשר להרים את השקף מהשולחן, להזיז אותו באוויר, ולהחזיר לשולחן בסוף. על פניו אני לא מוסיף כאן משהו חדש בנוסף לסיבוב והזזה אם מסתכלים רק על המיקום הסופי של השקף, אבל למעשה אפשר לעשות עוד משהו - להחזיר את השקף לשולחן כשהוא הפוך. האפקט של זה יהיה מה שנקרא שיקוף:

פעולת השיקוף היא הסיבה שבגללה אני מספר את הסיפור הזה עם שקף ולא עם סתם עצם דו-ממדי כמו דף רגיל. דף נייר עם ציור עליו הוא לא בדיוק אובייקט דו ממדי אלא תלת ממדי דק מאוד: קונספטואלית יש לו שתי שכבות לפחות, אחת של “קדימה” ואחת של “אחורה” שמסתירות זו את זו. לכן כשאנחנו הופכים דף אנחנו מעלימים שכבה אחת וחושפים את האחרת. בשקף נוצרת האשליה של שכבה בודדת, ואז היפוך משיג את האפקט של פעולת השיקוף.

מה עוד אתם יכולים לעשות עם השקף? יש לי שתי תשובות אפשריות לכך:

1. כלום. אלו כל הפעולות שאתם יכולים לעשות איתו.
2. אתם יכולים לפרק את השקף לאטומים בודדים ולהרכיב אותו חזרה בכל דרך מופרעת שתחשבו עליה.

אם תבקשו ממני לנסח מתמטית את ההבדל בין 1 ובין 2 אני אגיד שבדרך פעולה 2, אתם עלולים לקלקל תכונה כלשהי של השקף המקורי - לשנות את המרחק בין נקודות על השקף. הרעיון הוא שאם נבחר שתי נקודות אקראיות על השקף, נמדוד את המרחק ביניהן, ואז נבצע עליו את הפעולות שלנו ולבסוף נמדוד את המרחק בין המיקום החדש של שתי הנקודות, נקבל את אותו מרחק. לכל זוג נקודות. לפונקציות שמשמרות מרחקים באופן כזה קוראים איזומטריות, ובהקשר שלנו של איזומטריות של \( \mathbb{R}^{2} \) קוראים להן גם “תנועות צפידות” או “תנועות קשיחות”, כשהאינטואיציה היא לחשוב עליהן בתור דרכי התנועה של גוף קשיח, שלא יכול להתחיל להתפרק פתאום לאטומים ולהרכיב את עצמו מחדש.

התנועות הצפידות הן דוגמה חשובה לחבורה: אפשר להרכיב אותן ולקבל תנועה צפידה חדשה, וכל תנועה אפשר “לבטל” על ידי תנועה נגדית. תנועת ה”יחידה” היא כמובן זו שלא מזיזה כלום. יש עוד כמה סיבות שבגללן זו חבורה מעניינת: היא לא אבלית, למשל כי סיבוב ואז שיקוף שונה משיקוף ואז סיבוב:

היא לא בת מניה כי למשל עבור סיבוב בכל זווית שהיא מספר ממשי בין 0 ל-\( 2\pi \) נקבל תנועה קשיחה אחרת; והיא דוגמה מאוד ויזואלית לאופן שבו חבורה פועלת על קבוצה כלשהי. כאן המהות של החבורה היא לעשות משהו לנקודות של \( \mathbb{R}^{2} \): כל איבר בחבורה הוא טרנספורמציה של \( \mathbb{R}^{2} \) ופעולת ה”כפל” של החבורה היא בעצם פעולת הרכבה של טרנספורמציות. הנושא של מה קורה כשלוקחים חבורה ומפעילים אותה על קבוצה הוא חשוב ומרכזי למדי - מהר מאוד רואים שלומדים מכך משהו גם על הקבוצה וגם על החבורה, כתלות בשתיהן. אני אדבר על זה יותר בפוסט בהמשך; בינתיים אני רוצה לדבר עוד קצת על תנועות צפידות.

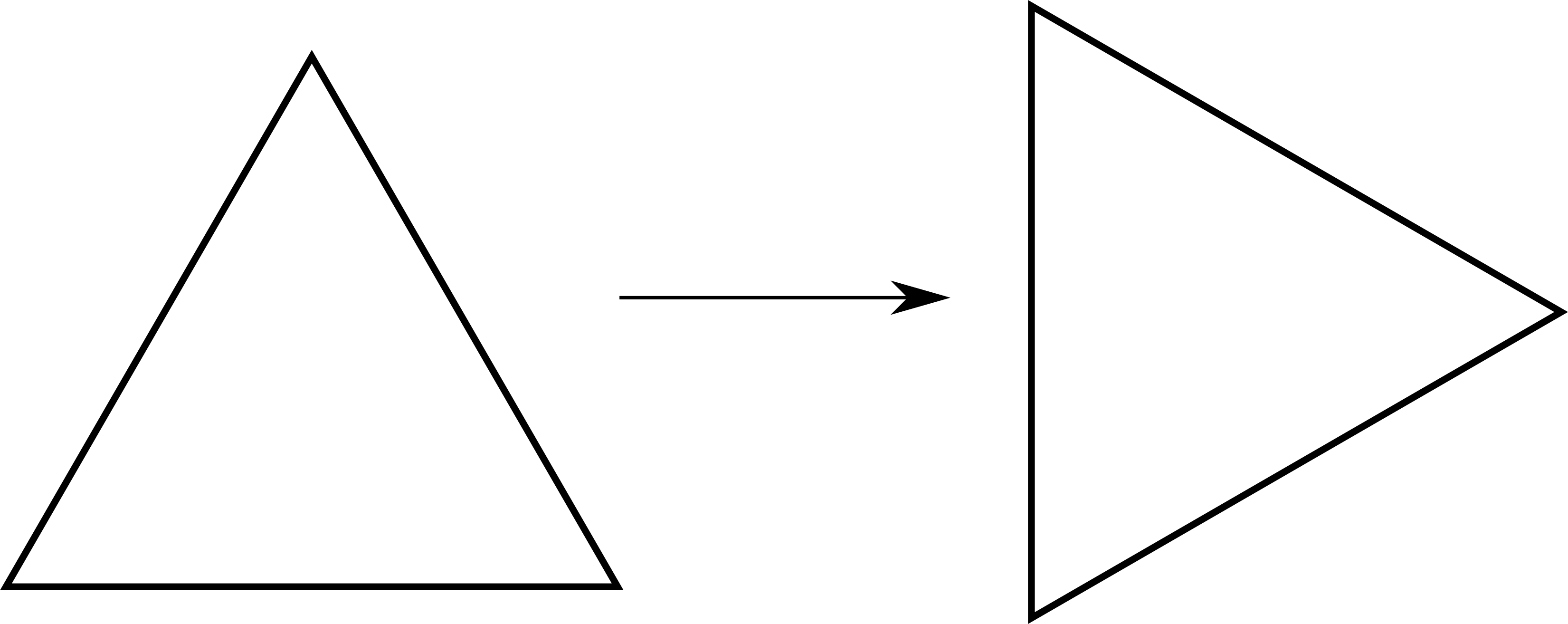
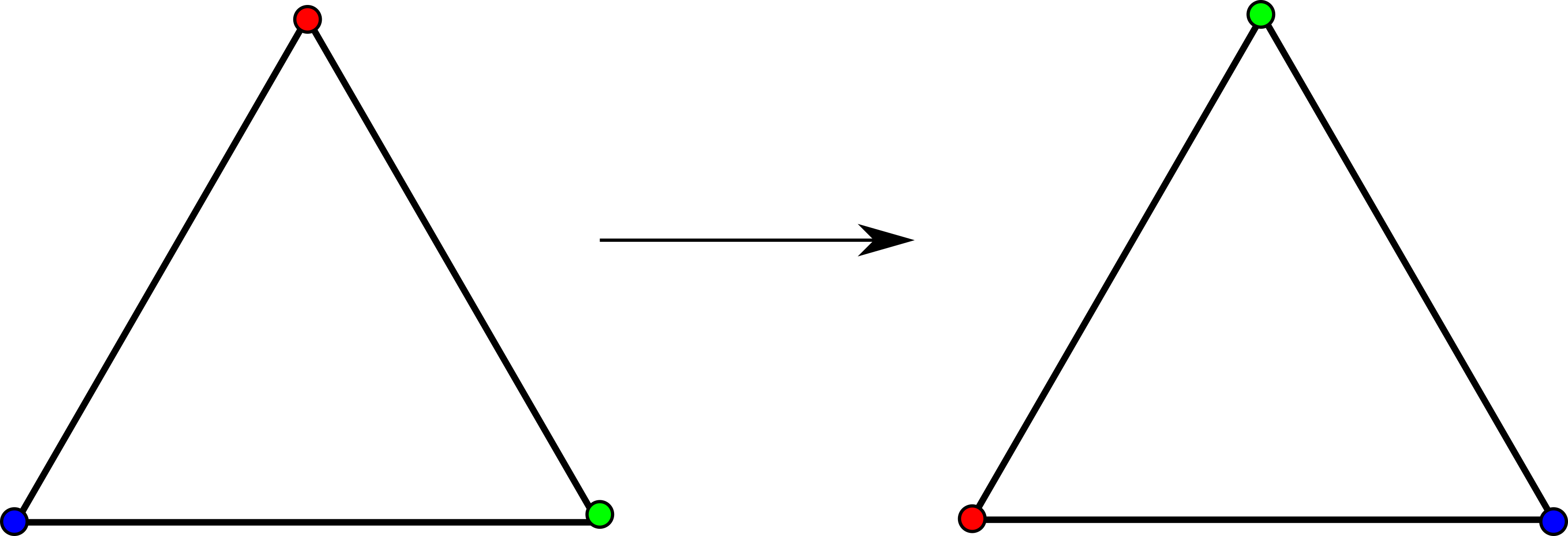
אני חושב על תנועה צפידה בתור פונקציה שפועלת על כל \( \mathbb{R}^{2} \). פונקציה כזו מוגדרת “נקודתית”, אבל אפשר כמובן לשאול את עצמנו מה היא עושה לקבוצה של נקודות. זו אפילו הדרך שבה קל לנו בדרך כלל לדמיין פעולות. הנה למשל מה קורה כשלוקחים משולש שווה צלעות ומפעילים עליו סיבוב ב-90 מעלות ביחס למרכזו:

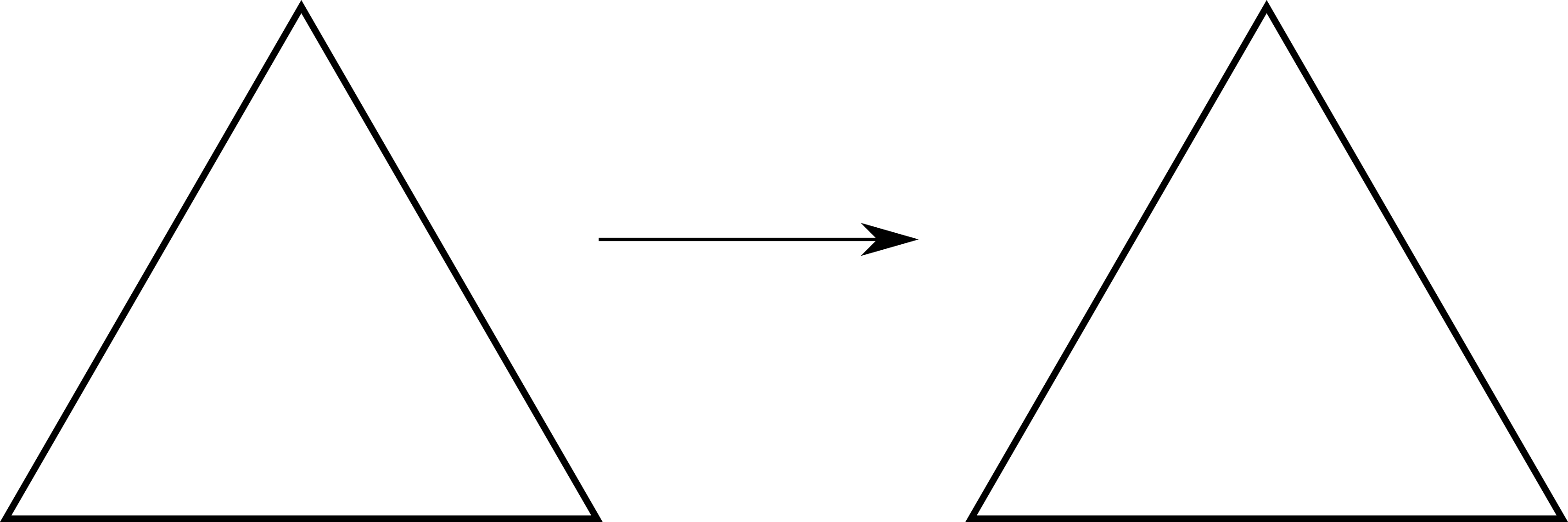
ומה יהיה אם נעשה סיבוב של 120 מעלות? נקבל את זה:

מה קורה פה? שום דבר לא השתנה. אם משולש מסתובב ביער ב-120 מעלות ואף אחד לא רואה, האם הוא הסתובב? מנקודת מבט אחת, לא; התוצאה הסופית נראית כמו המקור. מצד שני, היא כן: אם נסתכל על הנקודות הבודדות שמרכיבות את המשולש, כולן זזו. בואו נצבע לרגע את הקודקודים שלו בצבעים ונראה איך הסיבוב השפיע עליהם:

כלומר, הסיבוב ביצע “ערבוב” של הקודקודים. בלשון שאנחנו כבר מכירים, אם הקודקודים ממוספרים על ידי 1,2,3, הרי שהסיבוב הזה פעל על הקודקודים כמו התמורה \( \left(1\ 2\ 3\right) \). אז יש לנו כאן ביד פונקציה מעניינת: מצד אחד היא מבצעת שינוי לא טריוויאלי של הנקודות הבודדות שמרכיבות את המשולש, ומצד שני היא משאירה את המשולש ככללותו ללא שינוי. לפונקציה כזו קוראים סימטריה.

בלשון יומיומית, כשאנחנו אומרים שמשהו הוא “סימטרי” אנחנו מתכוונים בדרך כלל לכך שאפשר לחלק אותו לשני חלקים שאחד מהם הוא שיקוף של השני. במילים אחרות, שקיים ציר שביחס אליו, פעולת השיקוף היא סימטריה של המשהו. בלשון המתמטית אנחנו מרשים קצת יותר מזה - גם צורה שאפשר לסובב אותה והיא נשארת אותו דבר היא “סימטרית”. למשל:

וגם צורה שאפשר להזיז אותה בלי שהיא תשתנה היא “סימטרית”. רגע, מה? איך אפשר להזיז צורה מבלי שהיא תשתנה? ובכן, אם מדובר על צורה אינסופית, למשל על חצי מהמישור. נאמר שכולו נראה ככה:

אבל אני רוצה לדבר הפעם על סוג מאוד ספציפי של סימטריות - כאלו של המשולש שווה הצלעות וההכללות שלו. מה שמיוחד במשולש שווה צלעות הוא שמדובר על מצולע משוכלל - כל הצלעות שלו מאותו האורך, וכל הזוויות שלו הן מאותו גודל. עבור מרובעים הצורה המשוכללת נקראת ריבוע (במלבן כל הזוויות מאותו גודל אבל לא כל הצלעות מאותו אורך בהכרח; במעוין כל הצלעות מאותו אורך אבל לא כל הזוויות מאותו גודל בהכרח). עבור מחומשים, משושים וכן הלאה כבר פשוט משתמשים בשם “מחומש משוכלל”, “משושה משוכלל” וכן הלאה.

בואו ניקח מצולע משוכלל בעל \( n \) צלעות, ולכן בעל \( n \) קודקודים, ונמספר את הקודקודים הללו בתור \( \left\{ 1,2,\dots,n\right\} \). סימטריה של המצולע בפרט תעביר קודקודים לקודקודים, ולכן אפשר לחשוב עליה בתור פרמוטציה של \( \left\{ 1,\dots,n\right\} \), אבל לא כל פרמוטציה תעבוד פה. בואו נשאל את עצמנו ראשית כל לאן \( 1 \) יכול ללכת. בבירור אנחנו יכולים לבצע סיבוב של הצורה סביב המרכז שלה. סיבוב של \( \frac{360}{n} \) מעלות יעביר את \( 1 \) אל הקודקוד \( 2 \), את הקודקוד 2 אל 3 וכן הלאה. עוד סיבוב כזה יעביר את 1 אל 3, וכן הלאה וכן הלאה. במילים אחרות, לכל \( 1\le k\le n \) יש לנו סימטריה שמעבירה את 1 אל \( k \). עכשיו, נניח ש-\( 1 \) עבר אל \( k \), לאן 2 יכול לעבור? מכיוון שסימטריה היא תנועה קשיחה, המרחק של 2 מ-1 חייב להישאר קבוע. כלומר, 2 יכול לעבור רק אל \( k-1 \) או אל \( k+1 \). אם ביצענו סיבוב ותו לא, אז 2 עבר אל \( k+1 \). אבל אחרי ביצוע הסיבוב הזה אנחנו יכולים לבצע גם שיקוף: נעביר את ציר השיקוף דרך \( k \) ומרכז המצולע, ונקבל ש-\( 2 \) עובר ל-\( k-1 \). במילים אחרות, לכל \( 1\le k\le n \) יש לנו שתי סימטריות שונות שמעבירות את \( 1 \) אל \( k \): האחת שמעבירה את 2 אל \( k-1 \) והשניה שמעבירה אותו אל \( k+1 \). כעת, מכיוון שסימטריה היא תנועה קשיחה לא קשה להראות שאחרי שקבענו לאן \( 1,2 \) הולכים, כל יתר הקודקודים נקבעים באופן יחיד.

אם כן, קיבלנו שחבורת הסימטריות של מצולע משוכלל בן \( n \) צלעות כוללת בדיוק \( 2n \) איברים: \( n \) איברים שהם סיבובים, ועוד \( n \) איברים שהם סיבוב-ואז שיקוף. את החבורה הזו מסמנים, בהתאם, בתור \( D_{2n} \) והיא נקראת “החבורה הדיהדרלית מסדר \( 2n \)”.

הסיבה המרכזית שבגללה החבורה הזו מעניינת אותי כרגע היא שזו הזדמנות טובה לראות תיאור של חבורה באמצעות יוצרים ויחסים. את האינטואיציה כבר יש לנו: ראינו שאפשר לתאר כל איבר של החבורה באמצעות הפעלות נשנות של סיבוב ב-\( \frac{360}{n} \) מעלות, ואז ביצוע פעולת שיקוף. הציר של השיקוף השתנה בכל פעם, אבל למעשה זה מיותר - אפשר פשוט לשקף בהתחלה תמיד ביחס לציר שעובר דרך 1 ומרכז המצולע. לכן אפשר להגדיר שני איברים \( s,r\in D_{2n} \): \( r \) הוא הסיבוב ואילו \( s \) הוא השיקוף. קל לראות שהסדר של \( r \) הוא \( n \), כלומר האיברים \( r,r^{2},r^{3},\dots,r^{n} \) כולם שונים זה מזה. כמו כן \( s^{2}=e \), כמובן (שיקוף תמיד מבטל את עצמו), ואפשר לכתוב את כל החבורה כך:

\( D_{2n}=\left\{ e,r,r^{2},\dots,r^{n-1},s,sr,sr^{2},\dots,sr^{n-1}\right\} \).

אם בחרתי את הייצוג הזה לאברי החבורה, עולה השאלה איך כופלים אותם. כפל כמו \( \left(sr^{2}\right)\cdot r^{3} \) קל לבצע, פשוט משתמשים באסוציאטיביות: \( s\left(r^{2}r^{3}\right)=sr^{5} \). אבל איך מבצעים, למשל, את הכפל \( \left(sr\right)\left(sr^{2}\right) \)? החבורה היא לא אבלית. אי אפשר סתם להחליף את סדר המוכפלים ולהגיד שקיבלנו \( s^{2}r^{3}=r^{3} \) כי זה לא יהיה נכון. אנחנו בעצם רוצים להבין איך אפשר להחליף את \( rs \) במשהו אחר שבו \( s \) בצד שמאל ו-\( r \) בצד ימין. בדיקה ישירה מראה שמתקיים \( rs=sr^{-1} \), וקל להכליל את זה אל \( r^{k}s=sr^{-k} \). לכן את הכפל לעיל אפשר לבצע כך: \( \left(sr\right)\left(sr^{2}\right)=s\left(rs\right)r^{2}=ssr^{-1}r^{2}=r \).

בואו נדבר עכשיו בצורה כללית יותר. אם יש לנו חבורה כלשהי, ויש בה איבר כלשהו \( a \), אז אנחנו יודעים בודאות שבחבורה שלנו יהיו כל האיברים מהצורה \( a,a^{2},a^{3},\dots \) וגם \( a^{0},a^{-1},a^{-2},\dots \). כמובן, אולי חלק מהאיברים הללו יהיו זהים זה לזה, אבל כולם יופיעו בחבורה. ועכשיו בואו נעשה את זה למקרה שבו יש שני איברים \( a,b \). אז עכשיו צריך להתייחס לא רק לחזקות שלהם, אלא גם למכפלות של חזקות שלהם. גם ביטוי כמו \( aba \) הופך לרלוונטי, וגם \( a^{4}b^{-2}ab^{7} \) וכדומה. לביטוי כזה אני קורא בשם מילה מעל \( a,b \). הוא בסך הכל סדרה של חזרות כלשהן על \( a,b \) ועל \( a^{-1},b^{-1} \) (תוך קיצור \( aaa \) ל-\( a^{3} \) וכדומה). על \( e \) אפשר לחשוב פשוט בתור “סדרה ריקה” שלא כוללת איברים כלל.

אם רוצים, אפשר להגדיר ככה חבורה: אוסף כל המילים מעל \( a,b \), כאשר “כפל” הוא פשוט שרשור של מילים, וכמו כן מתבצע “צמצום” על ידי כך שמוחקים מהמילה זוגות סמוכים של תווים מהצורה \( aa^{-1} \) או \( a^{-1}a \). החבורה שמתקבלת בצורה הזו נקראת החבורה החופשית על שני איברים, וה-\( a,b \) נקראים היוצרים שלה. מן הסתם אפשר להכליל את ההגדרה הזו לקבוצה כלשהי של יוצרים, לאו דווקא סופית.

החבורה החופשית על שני איברים היא בוודאי לא \( D_{2n} \). הרי היא אינסופית ואילו \( D_{2n} \) סופית. אם אנחנו רוצים להגיע למקומות מעניינים עם ייצוג של חבורות באמצעות יוצרים באופן הזה, אנחנו צריכים להכניס למשחק גם יחסים. פורמלית אפשר לחשוב על יחס בתור “כלל שכתוב” - אם יש תת-מילה כלשהי, אפשר להחליף אותה בתת-מילה אחרת. יחס מיוצג על ידי שוויון שמייצג את שתי תתי-המילים שאפשר להחליף. עבור החבורה הדיהדרלית יש לנו שלושה יחסים: \( s^{2}=e \) (כלומר, אפשר להחליף את תת-המילה \( ss \) במילה ריקה - “למחוק אותה”) \( r^{n}=e \) ו- \( rs=sr^{-1} \). פרט לאלו יש לנו את כללי השכתוב שקיימים “אוטומטית” בכל חבורה: \( rr^{-1}=r^{-1}r=e \) ו-\( ss^{-1}=s^{-1}s=e \). כלומר אפשר לצמצם מופעים סמוכים של איבר וההופכי שלו, או ליצור אותם יש מאין.

כתיב פורמלי מקובל לתיאור של חבורה עם יוצרים ויחסים הוא באמצעות סוגריים משולשים, כשהיוצרים כתובים משמאל והיחסים מימין:

\( D_{2n}=\left\langle r,s|r^{n}=s^{2}=e,rs=sr^{-1}\right\rangle \)

וזה בעצם מסיים את זה - למדנו דרך חדשה להציג חבורות, אולי כאלו שקודם היה לנו מסובך למדי להציג. כמובן, את \( D_{2n} \) יכלתי להציג בתור תת-חבורת תמורות, אבל דרך ההצגה של יוצרים ויחסים היא נחמדה יותר לטעמי.