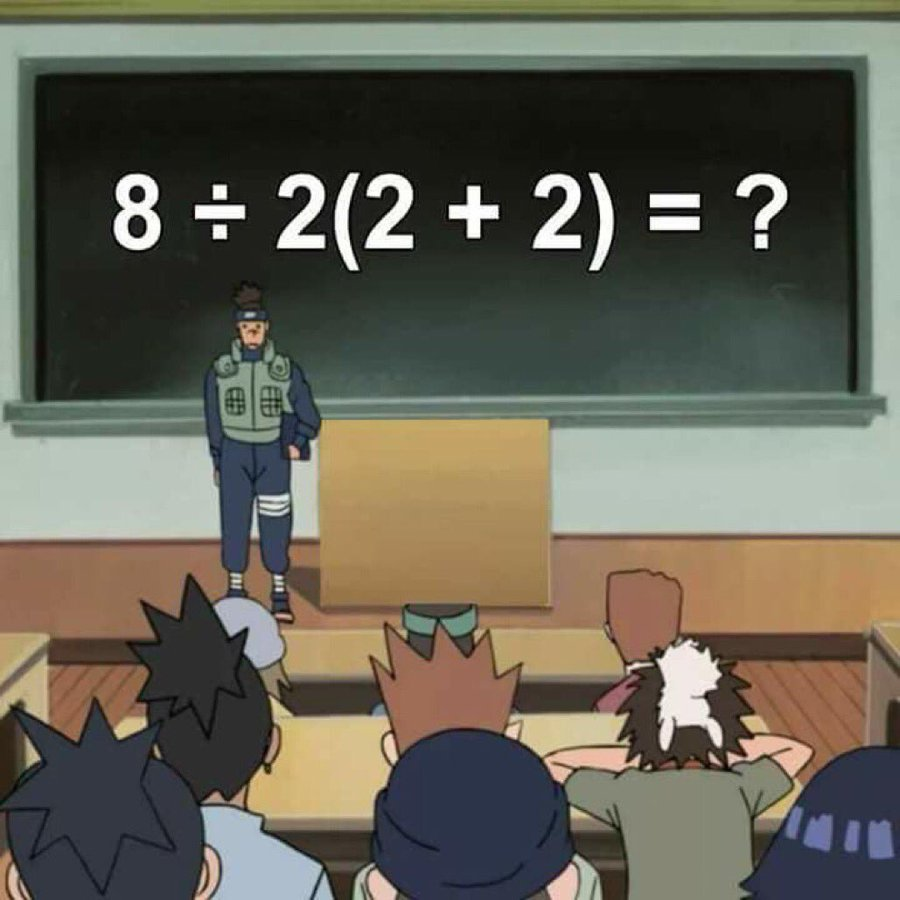ברוכות וברוכים הבאים אל הבלוג "לא מדויק". המטרה שלי כאן היא פשוטה - לספר על דברים במתמטיקה שמעניינים אותי, לתת את האינטואיציה שמאחוריהם ולהתלהב מהם. לא משנה אם זה חשבון של בית הספר היסודי, מתמטיקה של התיכון, לימודים אוניברסיטאיים או סתם חידות נחמדות - להכל יש מקום.
איך אני מעלה פוסטים לבלוג?
פוסטים אחרונים
טורי חזקות ורדיוס התכנסות
לא מדויק - בלוג על מתמטיקה ומדעי המחשב
מה כל הסיפור הזה עם הערך של פאי בתנ"ך?
לא מדויק - בלוג על מתמטיקה ומדעי המחשב
סדרות וטורים של פונקציות
לא מדויק - בלוג על מתמטיקה ומדעי המחשב
אז איך באמת פותרים משוואה ריבועית?
לא מדויק - בלוג על מתמטיקה ומדעי המחשב
חוקי החזקות
לא מדויק - בלוג על מתמטיקה ומדעי המחשב
פוסטים נבחרים
אז מה הקטע עם הנוסחה המעצבנת הזו?
האם (2+2)2÷8 שווה ל-16 או ל-1? תאמינו או לא, אבל הנוסחה המזעזעת הזו היא גלגול חדש של נוסחה ישנה יותר שכבר כתבתי עליה בבלוג. אז כמו עכשיו התשובה היא בעיקר תעזבו אותי באמא'שכם
מה זה בעצם מחשב קוונטי ולמה מתלהבים ממנו?
מחשבים קוונטיים משתמשים בעקרונות מופלאים באמת בפיזיקה כדי לבצע חישובים מאוד מסויימים בצורה יעילה יותר משאפשר לעשות במחשב רגיל. אבל התחום עדיין בחיתוליו ונפוצות עליו הרבה מיסקונספציות. אני מנסה לעשות קצת סדר בבלאגן.
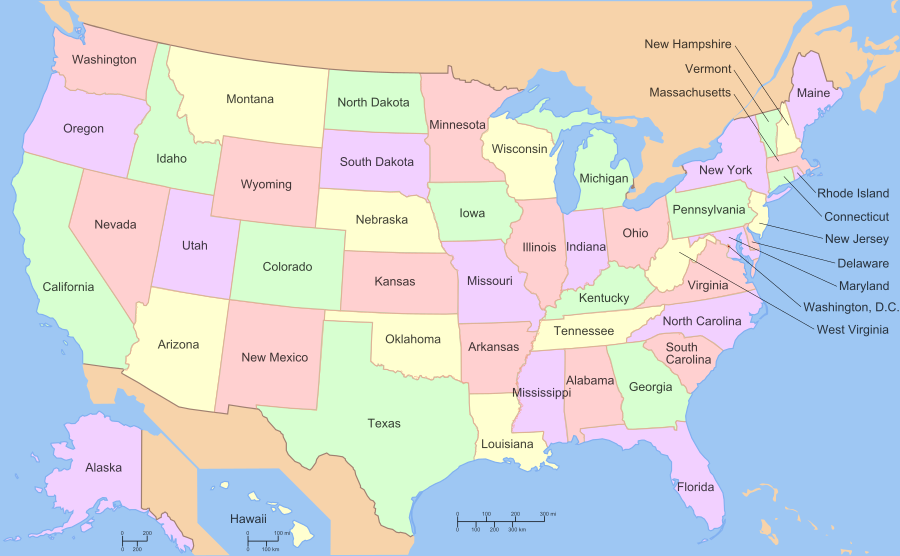
משפט ארבעת הצבעים
האם מספיקים ארבעה צבעים כדי לצבוע כל מפה כך שאין שתי מדינות סמוכות הצבועות באותו הצבע? לכאורה שאלה פרקטית קלילהלה שהתעוררה מנסיון מעשי לצבוע את מפת אנגליה; בפועל מפלצת מתמטית שהוליכה את הקהילה שולל במשך קרוב למאה שנים ולבסוף נפתרה רק באמצעות מחשבים.