בואו נדבר על מכפלות של חבורות וחבורות אבליות

מכפלה של חבורות

את סדרת הפוסטים על חבורות התחלנו בלהסביר מה זו חבורה, ואז לנסות להבין איך נראות החבורות הקטנות ביותר, להסתבך, להתייאש ולעבור לדברים אחרים, תיאורטיים וכלליים יותר. עכשיו אני רוצה לחזור לשאלת “אילו חבורות יש”. כפי שכבר ראינו, חלק מהבעיה עם מענה לשאלה הזו היא שקשה לנו לתאר חבורות. לכתוב טבלת כפל זה מאוד מסורבל וקשה מאוד להבין איך החבורה “מתנהגת” מתוך טבלת הכפל. לכן אני הולך להקדיש את הפוסט הזה לתיאור של כמה דרכים אחרות לייצוג של חבורות שאחרי שנשלוט בהן יאפשרו לנו להבין די טוב איך נראות הרבה מאוד חבורות - בפרט, נוכל להבין בדיוק איך נראות כל החבורות האבליות הסופיות (ואפילו חבורות אבליות קצת יותר מסובכות).

בואו נתחיל עם משהו שכבר ראינו בפוסטים קודמים בנפנוף ידיים - מכפלה ישרה (או סתם “מכפלה”) של חבורות. אם \( A,B \) הן חבורות כלשהן, אז אפשר לבנות מתוכן חבורה חדשה, \( A\times B \), שהאיברים שלה הם הזוגות מהצורה \( \left(a,b\right) \) כך ש-\( a\in A \) ו-\( b\in B \) והפעולה שמוגדרת עליה היא כפל “על פי קואורדינטות”, כלומר \( \left(a,b\right)\cdot\left(x,y\right)=\left(ax,by\right) \) כאשר \( ax \) הוא מה שקורה כשמכפילים את \( a,x\in A \) על פי פעולת הכפל שמוגדרת על החבורה \( A \) ואת \( b,y\in B \) על פי פעולת הכפל שמוגדרת על החבורה \( B \). במילים אחרות, בחבורה \( A\times B \) הקואורדינטות השונות הן “בלתי תלויות” - הן לא משפיעות זו על זו (להבדיל, למשל, מבניה אחרת שנקראת מכפלה חצי ישרה ואראה בהמשך). הדוגמה הקלאסית ביותר לבניה הזו היא המישור \( \mathbb{R}^{2} \) שהוא בעצם \( \mathbb{R}\times\mathbb{R} \) עם פעולת החיבור הרגילה של וקטורים.

אם אנחנו יודעים להגדיר חיבור על מכפלה קרטזית של שתי קבוצות, אפשר לעשות את אותו הדבר למכפלה של מספר כלשהו של קבוצות, גם אינסופי. אני אתן את שני המקרים הפשוטים: אם \( A_{1},\dots,A_{n} \) הן חבורות אז \( A_{1}\times\dots\times A_{n} \) היא חבורה שכל איבר בה הוא מהצורה \( \left(a_{1},\dots,a_{n}\right) \) כך ש-\( a_{i}\in A_{i} \) וכפל הוא נקודתי: \( \left(a_{1},\dots,a_{n}\right)\cdot\left(b_{1},\dots,b_{n}\right)=\left(a_{1}b_{1},\dots,a_{n}b_{n}\right) \). באופן דומה, אם \( A_{1},A_{2},\dots \) הן אינסוף (בן-מניה, אם הביטוי הזה אומר לכם משהו) חבורות אז \( A_{1}\times A_{2}\times\dots \) היא חבורה שכל איבר בה הוא מהצורה \( \left(a_{1},a_{2},\dots\right) \) כך ש-\( a_{i}\in A_{i} \) וכפל הוא נקודתי: \( \left(a_{1},a_{2},\dots\right)\cdot\left(b_{1},b_{2},\dots\right)=\left(a_{1}b_{1},a_{2}b_{2},\dots\right) \). אלו כאמור מקרים פשוטים יחסית - אני סומך על אלו מכם שיודעים איך מוגדרות מכפלות קרטזיות כלליות שידעו איך להגדיר מבנה של חבורה עליהן אם המוכפלים הם חבורות.

ייתכן שאתם מכירים שם שונה וסימון שונה למה שנראה כמו אותו הדבר - סכום ישר והסימון \( \oplus \). המושג הזה זהה למושג של מכפלה ישרה כאשר מפעילים אותו על מספר סופי של חבורות, אבל על מספר אינסופי שלהן, סכום ישר הוא מושג מגביל יותר: למשל, עבור \( A_{1}\oplus A_{2}\oplus\dots \) הוא דורש שבכל איבר \( \left(a_{1},a_{2},\dots\right) \) יתקיים \( a_{i}\ne e_{i} \) רק למספר סופי של איברים (כאשר \( e_{i} \) הוא איבר היחידה של \( A_{i} \)). למי שההבדל לא ברור לו, תחשבו על ההבדל בין טורי חזקות, שהם סכומים מהצורה \( \sum_{n=0}^{\infty}a_{n}x^{n} \) ובין פולינומים, שהם סכומים מהצורה \( \sum_{k=0}^{n}a_{k}x^{k} \) אבל אפשר גם לתאר אותם בתור סכומים מהצורה \( \sum_{n=0}^{\infty}a_{n}x^{n} \) כך שהחל ממקום מסויים \( a_{k}=0 \) לכל \( k \). בהמשך הפוסט נראה עוד דוגמא, עוד יותר טבעית, לדבר הזה. מכל מקום, כל עוד לא אזדקק להבחנה הזו אני אדבר אך ורק על מכפלות ישרות.

יש עוד סוג של מכפלה שאני רוצה לדבר עליו. המכפלה הישרה שהצגתי היא “חיצונית” - לוקחים שתי חבורות שלא קשורות אחת לשניה ובונים מהן חבורה חדשה. אבל אפשר לדבר גם על סוג שונה של מכפלה, שנראה אולי לא קשור במבט ראשון - אם \( G \) היא חבורה ו-\( A,B \) שתי תת-חבורות שלה, אפשר לכפול את שתי תת-החבורות: להגדיר קבוצה \( AB=\left\{ ab\ |\ a\in A,b\in B\right\} \). כאן אנחנו לא שומרים את \( a,b \) בתור איברים נפרדים בתוך זוג \( \left(a,b\right) \) אלא כופלים אותם, מקבלים איבר ב-\( G \) (שבהחלט ייתכן שלא יהיה שייך לא ל-\( A \) ולא ל-\( B \)) ומכניסים את האיבר הזה לקבוצה שהיא \( AB \). את ההגדרה הזו אפשר להגדיר תמיד, אבל האם תמיד נקבל כך חבורה חדשה? בפרט, האם תמיד נקבל משהו שאיזומורפי ל-\( A\times B \)? התשובה היא לחלוטין לא אבל לפעמים כן.

בואו נראה כמה דוגמאות פשוטות. נסתכל למשל על \( \mathbb{Z}_{6}=\left\{ 0,1,2,3,4,5\right\} \) עם פעולת החיבור מודולו 6. יש לה שתי תתי-חבורות לא טריוויאליות: \( A=\left\{ 0,2,4\right\} \) ו-\( B=\left\{ 0,3\right\} \). על פי הגדרת המכפלה, נקבל \( AB=\left\{ 0,2,4,3,5,1\right\} \), כאשר את האיברים חישבתי על ידי כך שקודם כל לקחתי את כל אברי \( A \) ו”כפלתי” אותם ב-\( 0\in B \) (“כפלתי”, כי בעצם ביצעתי חיבור מודולו 6) ואחר כך לקחתי את כל אברי \( A \) וכפלתי ב-\( 3\in B \). אפשר לראות שקיבלתי באופן הזה את כל אברי \( \mathbb{Z}_{6} \), כלומר \( AB=\mathbb{Z}_{6} \). כמו כן, \( A\cong\mathbb{Z}_{3} \) ו-\( B\cong\mathbb{Z}_{2} \) ואפשר לראות די בקלות ש-\( \mathbb{Z}_{3}\times\mathbb{Z}_{2}\cong\mathbb{Z}_{6} \) (האיבר \( \left(1,1\right) \) הוא היוצר של \( \mathbb{Z}_{3}\times\mathbb{Z}_{2} \)). כלומר, קיבלנו ש-\( AB\cong A\times B \) במקרה הזה.

מצד שני, בואו נסתכל על \( \mathbb{Z}_{8}=\left\{ 0,1,2,3,4,5,6,7\right\} \) עם חיבור מודולו 8 ועל תתי-החבורות \( A=\left\{ 0,2,4,6\right\} \) ו-\( B=\left\{ 0,4\right\} \). במקרה הזה נקבל \( AB=\left\{ 0,2,4,6\right\} \) ותו לא, כי חיבור של 4 עם אברי \( A \) יתן לנו בדיוק את אברי \( A \). זה לא מפתיע - הרי \( 4\in A \) בעצמו. המסקנה? במקרה הנוכחי \( AB=A \), ולכן בוודאי ש-\( AB\not\cong A\times B \). איך זה יכול להיות? הרי ב-\( AB \) רק ארבעה איברים וב-\( A\times B \), על פי ההגדרה, יש שמונה איברים.

אם כן, אנחנו רואים שיכולה להיות בעיה כבר כשמדברים על מספר האיברים. זה מוביל אותנו לשאלה מספר 1: אם \( A,B \) סופיות, מהו מספר האיברים ב-\( AB \)? התשובה פשוטה: \( \left|AB\right|=\frac{\left|A\right|\cdot\left|B\right|}{\left|A\cap B\right|} \). למה? ובכן, קוסטים. זוכרים שהיה פעם משהו כזה?

קוסט של \( B \), כזכור, הוא קבוצה מהצורה \( aB=\left\{ ab\ |\ b\in B\right\} \). מההגדרה הזו קל לראות ש-\( AB=\bigcup_{a\in A}aB \), כלומר המכפלה \( AB \) היא בעצם איחוד של קוסטים של \( B \). ראינו בעבר שקוסטים הם או זרים או שווים - אין שני קוסטים שיש להם “קצת” איברים משותפים ותו לא. יותר מכך - הגודל של כל הקוסטים שווה לגודל של \( B \): \( \left|aB\right|=\left|B\right| \) לכל \( a \). לכן השאלה היחידה היא כמה קוסטים שונים זה מזה של \( B \) משתתפים באיחוד. לשם כך, בואו ניזכר מתי שני קוסטים הם שווים: \( a_{1}B=a_{2}B \) אם ורק אם \( a_{1}a_{2}^{-1}\in B \). מכיוון ש-\( a_{1},a_{2}\in A \) ו-\( A \) היא תת-חבורה, אז \( a_{1}a_{2}^{-1}\in A \). המסקנה היא ש-\( a_{1}a_{2}^{-1}\in A\cap B \), כלומר ש-\( a_{1}\left(A\cap B\right)=a_{2}\left(A\cap B\right) \). במילים: שני איברים של \( A \) מגדירים את אותו קוסט של \( B \) ב-\( G \) אם ורק אם הם מגדירים את אותו קוסט של \( A\cap B \) (שהיא תת-חבורה של \( A \)) ב-\( A \). מספר הקוסטים של \( A\cap B \) ב-\( A \) הוא בדיוק \( \frac{\left|A\right|}{\left|A\cap B\right|} \) ומכאן נובע המשפט.

אם כן, אנחנו רואים שתנאי הכרחי לכך ש-\( AB \) יהיה איזומורפי ל-\( A\times B \) הוא ש-\( \left|A\cap B\right|=1 \), כלומר ש-\( A\cap B=\left\{ e\right\} \). אלו מכם שזוכרים קצת אלגברה לינארית בוודאי זוכרים שאפשר לקחת שני תתי-מרחבים וקטוריים \( U,V \) ולהגדיר \( U+V \) - זה בדיוק כמו כפל אצלנו, רק הסימון של הפעולה שונה - ושאומרים שאם בנוסף לכך \( U\cap V=\left\{ 0\right\} \) אז את הסכום הזה מסמנים ב-\( U\oplus V \) וקוראים לו סכום ישר של תתי-מרחבים. זה בדיוק מה שאנחנו מדברים עליו גם כאן.

העניין הוא שזה לא תנאי מספיק כי בכלל לא בטוח ש-\( AB \) תהיה תת-חבורה של \( G \). עבור חבורה אבלית זו תהיה תת-חבורה, כפי שתכף אסביר, ולכן כדי לתת דוגמה נגדית אני חייב ללכת אל חבורות לא אבליות - בואו ניקח את הפשוטה ביותר שיש לי, \( S_{3} \), חבורת התמורות על \( \left\{ 1,2,3\right\} \). אני יודע ש-\( \left|S_{3}\right|=6 \) (זה תרגיל בסיסי בקומבינטוריקה), ועכשיו אני אגדיר שתי תתי-חבורות ציקליות של \( S_{3} \): \( A=\left\langle \left(1\ 2\right)\right\rangle ,B=\left\langle \left(2\ 3\right)\right\rangle \). מתקיים \( \left|A\right|=\left|B\right|=2 \) ומכיוון ש-\( A\cap B=\left\{ e\right\} \) נקבל ש-\( \left|AB\right|=4 \); זה אומר לי מיידית שלא ייתכן ש-\( AB \) היא תת-חבורה של \( S_{3} \) כי כל תת-חבורה של \( S_{3} \) צריכה להיות מגודל שמחלק את 6, על פי משפט לגראנז’.

בואו ננסה להוכיח ש-\( AB \) היא כן תת-חבורה, נראה איפה אנחנו נתקעים ונסיק מה חסר לנו. אני אשתמש, כרגיל, בקריטריון לתת-חבורה: אם \( a,b \) הם איברים של הקבוצה, אני צריך להוכיח ש-\( ab^{-1} \) הוא גם כן איבר שלה וזה מספיק. במקרה שלנו, כל איבר הוא בעצמו מכפלה, אז בואו נכתוב אותם בתור \( a_{1}b_{1} \) ו-\( a_{2}b_{2} \) ואני צריך להראות ש-\( \left(a_{1}b_{1}\right)\left(a_{2}b_{2}\right)^{-1}\in AB \). לא קשה לראות ש-\( \left(a_{2}b_{2}\right)^{-1}=b_{2}^{-1}a_{2}^{-1} \), כלומר קיבלנו את האיבר \( a_{1}b_{1}b_{2}^{-1}a_{2}^{-1} \). אם רק הייתי יכול להחליף את \( b_{1}b_{2}^{-1}a_{2}^{-1} \) ב-\( a_{2}^{-1}b_{1}b_{2}^{-1} \) הייתי מסיים - הייתי מקבל את האיבר \( \left(a_{1}a_{2}^{-1}\right)\left(b_{1}b_{2}^{-1}\right) \) שהוא מכפלה של איבר מ-\( A \) באיבר מ-\( B \). העניין הוא שאני לא יכול תמיד להחליף. אבל בוודאי שאני יכול אם \( G \) אבלית. אם \( G \) לא אבלית, מספיק לדרוש ש-\( AB=BA \) כדי שזה יעבוד (כלומר, שכל איבר שנכתב בתור \( ab \) יכול להיכתב גם בתור \( b^{\prime}a^{\prime} \) כאשר ייתכן ש-\( a^{\prime}\ne a \) וייתכן ש-\( b^{\prime}\ne b \)), ובפרט מספיק ש-\( A \) או \( B \) יהיו תתי-חבורות נורמליות כדי שזה יעבוד.

אם \( AB \) כן תת-חבורה ומתקיים \( A\cap B=\left\{ e\right\} \) אז אפשר לנסות להוכיח ש-\( AB\cong A\times B \). בואו נגדיר את ההומומורפיזם המתבקש: \( f:A\times B\to AB \) שמוגדר על ידי \( f\left(\left(a,b\right)\right)=ab \). כדי שזה יהיה הומומורפיזם צריך שיתקיים \( f\left(\left(a_{1}a_{2},b_{1}b_{2}\right)\right)=f\left(\left(a_{1},b_{1}\right)\right)f\left(\left(a_{2},b_{2}\right)\right) \), כלומר שיתקיים \( a_{1}a_{2}b_{1}b_{2}=a_{1}b_{1}a_{2}b_{2} \). זה אומר שאני חייב להיות מסוגל להחליף את \( a_{2}b_{1} \) ב-\( b_{1}a_{2} \). זה תנאי חזק יותר מהדרישה \( AB=BA \) או הדרישה ש-\( A \) או \( B \) יהיו נורמליות - בשני המקרים הללו אני יכול לבצע החלפה “בתשלום”, שמשנה את סדר האיברים ובתמורה מחליפה אותם באיברים אחרים מאותה תת-חבורה. כאן אני חייב שאלו יהיו אותם איברים. מסתבר שאם אני דורש ש-\( A,B \) יהיו שתיהן נורמליות, זה מספיק כדי להבטיח את זה - אראה את זה עוד רגע.

אם כן, עם התנאי הנוסף אנחנו מקבלים ש-\( f \) היא הומומורפיזם. בבירור \( f \) על, בשל ההגדרה של \( AB \). מה עם חד-חד-ערכיות? המשמעות של חד-חד-ערכיות כאן היא “לכל איבר ב-\( AB \) יש דרך הצגה יחידה כמכפלה של איבר מ-\( A \) באיבר מ-\( B \)” (שוב, אנשי אלגברה לינארית יזהו זאת מייד). בואו נניח ש-\( a_{1}b_{1}=a_{2}b_{2} \); אז נובע מכך ש-\( a_{1}a_{2}^{-1}=b_{2}b_{1}^{-1} \). אגף שמאל של המשוואה שייך ל-\( A \) ואגף ימין ל-\( B \) ולכן שני האגפים שייכים ל-\( A\cap B \), כלומר שווים ל-\( e \), וקיבלנו ש-\( a_{1}=a_{2} \) ו-\( b_{1}=b_{2} \). זה מסיים את ההוכחה.

ראינו שאם \( A,B \) שתיהן נורמליות אז \( AB\cong A\times B \). זה פותח פתח לשאלה מעניינת: האם ייתכן ש-\( AB \) היא כן תת-חבורה, אבל כזו שלא איזומורפית ל-\( A\times B \)? התשובה חיובית, ומעידה על כך שאנחנו צריכים עוד מושג של מכפלה, כללי יותר ממכפלה ישרה, כדי לתפוס את יתר המקרים. בשביל זה קיים המושג של מכפלה חצי ישרה שלא אציג כרגע אבל כנראה אגיע אליו בעתיד.

ועכשיו בואו ניקח את כל זה ונפעיל על חבורות אבליות.

משפט המיון לחבורות אבליות נוצרות סופית

בואו ניקח חבורה אבלית סופית \( G \). הנה הרעיון הבסיסי: \( G \) היא מכפלה ישרה של חבורות ציקליות. כלומר, אפשר לכתוב \( G\cong\mathbb{Z}_{n_{1}}\times\dots\times\mathbb{Z}_{n_{k}} \). צריך לשים לב לכך שדרך ההצגה הזו היא לאו דווקא יחידה. למשל \( \mathbb{Z}_{6}\cong\mathbb{Z}_{2}\times\mathbb{Z}_{3} \), אבל אפשר לבחור דרך הצגה קנונית באופן הבא: אם נדרוש ש-\( 1<n_{1}|n_{2}|\dots|n_{k} \) (כלומר, הגודל של כל חבורה במכפלה מחלק את הגודל של החבורה שאחריה וכל החבורות כוללות לפחות שני איברים) נקבל דרך הצגה אפשרית אחת; ואם נדרוש שהסדרים של כל החבורות במכפלה יהיו חזקות של ראשוניים, אז נקבל דרך הצגה אפשרית אחת. עבור החבורה הטריוויאלית \( \mathbb{Z}_{1}=\left\{ e\right\} \) אפשר לחשוב עליה כמיוצגת על ידי מכפלה “ריקה”, אם מישהו ממש רוצה להתעקש. דרך ההצגה הראשונה נקראת הצגה על ידי גורמים אינוריאנטיים (הגורמים האינוריאנטיים הם הסדרה \( n_{1},\dots,n_{k} \)) והשניה נקראת הצגה על ידי מחלקים אלמנטריים.

בואו נשתמש במשפט הזה לרגע כדי להבין מיהן כל החבורות האבליות מסדר 4, מה שאנחנו כבר יודעים כי חישבנו בצורה אחרת קודם. אם \( G\cong\mathbb{Z}_{n_{1}}\times\dots\times\mathbb{Z}_{n_{k}} \) אז \( \left|G\right|=\prod_{k=1}^{k}n_{i} \) ולכן במקרה שלנו הגורמים המוכפלים חייבים להיות מחלקים של 4, כלומר או שיהיה גורם יחיד שהוא 4, או שיהיו שני גורמים, שהם 2 ו-2. בצורה הזו אנחנו מקבלים שתי חבורות אבליות: \( \mathbb{Z}_{4} \) הציקלית, ו-\( \mathbb{Z}_{2}\times\mathbb{Z}_{2} \) שאינה ציקלית. אפילו בלי שנבדוק ש-\( \mathbb{Z}_{2}\times\mathbb{Z}_{2} \) אינה ציקלית המשפט כבר אומר לנו שהיא לא איזומורפית ל-\( \mathbb{Z}_{4} \) כי יש רק דרך הצגה אחת לכל אחת מהחבורות הללו בתור מכפלה של חבורות ציקליות שהסדר שלהן הוא חזקה של ראשוני (עבור \( \mathbb{Z}_{4} \) ההצגה הזו היא \( \mathbb{Z}_{2^{2}} \), וזו הצגה שונה מ-\( \mathbb{Z}_{2}\times\mathbb{Z}_{2} \)).

למשפט, אם כן, יש שני חלקים שונים:

1. כל חבורה אבלית היא מכפלה של חבורות ציקליות.
2. המכפלה הזו היא יחידה עד כדי כך-וכך.

אני לא הולך להוכיח את המשפט כאן. הסיבה לכך היא שהמשפט יכול להתקבל כמקרה פרטי של משפט כללי הרבה יותר באלגברה מופשטת - משפט המיון למודולים נוצרים סופית מעל תחום ראשי - שהוא משפט יפה במיוחד כי הוא נותן כמקרה פרטי גם תוצאות לא טריוויאליות מאלגברה לינארית - את הצורה הרציונלית וצורת ז’ורדן של מטריצות (שטרחתי לא מזמן להוכיח במפורש בבלוג - הוכחה די דומה להוכחה של משפט המיון הכללי, ודי דומה למה שאעשה אם ארצה להוכיח את המשפט עבור חבורות אבליות).

המשפט הזה מחסל, בעצם, את השאלה מיהן החבורות האבליות הסופיות. אנחנו יודעים בדיוק מיהן ואיך כולן נראות. הוא נותן לנו אלגוריתם שבהינתן מספר \( n \) יכול לייצר את כל החבורות האבליות מסדר \( n \) (לא אתן כרגע אלגוריתם אופטימלי שעושה את זה; אלגוריתם נאיבי סתם יכול לעבור על כל הסדרות של גורמים אינוריאנטים פוטנציאליים). בשביל הכיף, הנה סקירה זריזה של מיהן החבורות האבליות עבור סדר קטן יחסית (אני מציג אותן על פי גורמים אינוריאנטיים):

1. \( \mathbb{Z}_{1} \)
2. \( \mathbb{Z}_{2} \)
3. \( \mathbb{Z}_{3} \)
4. \( \mathbb{Z}_{4},\mathbb{Z}_{2}\times\mathbb{Z}_{2} \)
5. \( \mathbb{Z}_{5} \)
6. \( \mathbb{Z}_{6} \)
7. \( \mathbb{Z}_{7} \)
8. \( \mathbb{Z}_{8},\mathbb{Z}_{2}\times\mathbb{Z}_{4} \)
9. \( \mathbb{Z}_{9},\mathbb{Z}_{3}\times\mathbb{Z}_{3} \)
10. \( \mathbb{Z}_{10} \)
11. \( \mathbb{Z}_{11} \)
12. \( \mathbb{Z}_{12},\mathbb{Z}_{2}\times\mathbb{Z}_{6} \)
13. \( \mathbb{Z}_{13} \)
14. \( \mathbb{Z}_{14} \)
15. \( \mathbb{Z}_{15} \)
16. \( \mathbb{Z}_{16},\mathbb{Z}_{8}\times\mathbb{Z}_{2},\mathbb{Z}_{4}\times\mathbb{Z}_{4},\mathbb{Z}_{2}\times\mathbb{Z}_{2}\times\mathbb{Z}_{4},\mathbb{Z}_{2}\times\mathbb{Z}_{2}\times\mathbb{Z}_{2}\times\mathbb{Z}_{2} \)
17. \( \mathbb{Z}_{17} \)
18. \( \mathbb{Z}_{18}\mathbb{Z}_{3}\times\mathbb{Z}_{6} \)
19. \( \mathbb{Z}_{19} \)
20. \( \mathbb{Z}_{20},\mathbb{Z}_{2}\times\mathbb{Z}_{10} \)

אוקיי. מה עכשיו?

עד עכשיו דיברתי על חבורות סופיות, אבל מה עם חבורות אינסופיות? ובכן, בואו נתחיל שוב, מהפשוט ביותר. החבורה האבלית האינסופית הפשוטה ביותר היא \( \mathbb{Z} \) - החבורה הציקלית האינסופית היחידה. גם את \( \mathbb{Z} \) אפשר לכפול בעצמה - נסמן ב-\( \mathbb{Z}^{r} \) מכפלה של \( r \) עותקים של \( \mathbb{Z} \). עכשיו אפשר לדבר על חבורות שהן מהצורה \( \mathbb{Z}^{r}\times G \) כאשר \( G \) היא חבורה אבלית סופית. על \( G \) אפשר להשתמש במשפט המיון לחבורות אבליות סופיות, כך שאנחנו מקבלים משפט מיון רחב טיפה יותר - משפט המיון לחבורות אבליות נוצרות סופית. חבורה אבלית \( G \) היא נוצרת סופית אם קיימים בה איברים \( a_{1},\dots,a_{k} \) כך ש-\( G\subseteq\left\langle a_{1}\right\rangle \left\langle a_{2}\right\rangle \cdots\left\langle a_{k}\right\rangle \), כלומר אפשר לכתוב כל איבר ב-\( G \) בתור מכפלה של חזקות של האיברים \( a_{1},\dots,a_{k} \). כל חבורה סופית היא כמובן נוצרת סופית כי אפשר לקחת את כל אברי החבורה בתור יוצרים. משפט המיון אומר לנו שאם חבורה אבלית היא נוצרת סופית אז היא בהכרח מהצורה \( \mathbb{Z}^{r}\times G \) הזו - חשבו על כך כאילו החלק של \( \mathbb{Z}^{r} \) תופס את האיברים שהם מסדר אינסופי והחלק של \( G \) תופס את האיברים שהם מסדר סופי.

ללא-נוצרות-סופית ומעבר לו!

ובכן, טיפלנו בחבורות סופיות. טיפלנו בחבורות “קצת אינסופיות”. ומה עוד יש לנו? העולם הגדול הוא מסובך ואני לא מכיר את רובו בעצמי, אבל בואו ניתן כמה דוגמאות זריזות לחבורות אבליות לא נוצרות סופית, כדי שנכיר.

ראשית כל, מספרים עם פעולת חיבור. \( \mathbb{Z} \) הייתה חבורה אבלית נוצרת סופית, אבל כבר כשעוברים לקבוצת המספרים הבאה, \( \mathbb{Q} \), מקבלים חבורה לא נוצרת סופית. למה לא נוצרת סופית? כי לכל קבוצה סופית של שברים אפשר למצוא מכנה משותף. למשל, אם הייתי טוען ש-\( \frac{1}{2} \) ו-\( \frac{1}{3} \) יוצרים את כל הרציונליים, היו אומרים לי שכל צירוף לינארי שלהם הוא מהצורה \( \frac{3a+2b}{6} \) ועכשיו לכו תיצרו ככה את \( \frac{1}{7} \). צודקים.

הרציונליים מזכירים לנו חבורה מעניינת אחרת - חבורת שורשי היחידה. “שורש יחידה” הוא מספר מרוכב \( z \) כך ש-\( z^{n}=1 \) עבור \( n \) טבעי כלשהו. למשל, שורשי היחידה מסדר 2 הם \( 1 \) ו-\( -1 \), ושורשי היחידה מסדר 4 הם \( 1,-1,i,-i \). איך זה קשור לרציונליים? ובכן, דרך אפשרית אחת לכתוב מספרים מרוכבים היא בהצגה קוטבית, \( z=re^{i\theta} \) כך ש-\( \theta \) היא זווית שנתונה ברדיאנים ומתארת את הזווית של המספר המרוכב עם ציר \( x \) ו-\( r\ge0 \) מתאר את הערך המוחלט שלו. כאשר מעלים מספר מרוכב כזה בחזקה, מקבלים \( z^{n}=r^{n}e^{i\theta n} \), כך שאם אנחנו רוצים לקבל 1 אנחנו חייבים לדרוש \( r=1 \) ו-\( \theta n\equiv0\left(\text{mod }2\pi\right) \). במילים אחרות, \( 2\pi \) צריך לחלק את \( \theta n \) ובניסוח שקול, \( \frac{2\pi}{n} \) צריך לחלק את \( \theta \). עבור שורשי היחידה מסדר 4 זה אומר ש-\( \frac{2\pi}{4}=\frac{\pi}{2} \) צריך לחלק את \( \theta \) - מה שאנחנו קוראים לו ביומיום “\( \theta \) יכול להיות 0 מעלות או 90 מעלות או 180 מעלות או 270 מעלות”. מה שיוצא לנו מכל זה הוא ששורש יחידה הוא מספר מרוכב מהצורה \( e^{i2\pi\frac{k}{n}} \) עבור \( k\ge0 \) ו-\( n\ge1 \) טבעיים. פעולת הכפל של שני מספרים כאלו מתורגמת לחיבור של המעריכים שלהם. רואים מה קיבלנו? משהו שמזכיר מאוד את הרציונליים עם פעולת החיבור. אם נגדיר הומומורפיזם מ-\( \mathbb{Q} \) לחבורת שורשי היחידה על ידי \( \frac{k}{n}\mapsto e^{i2\pi\frac{k}{n}} \), מה יהיה הגרעין שלו? בדיוק המספרים הרציונליים שעבורם \( e^{i2\pi\frac{k}{n}}=1 \), כלומר ש-\( k \) הוא כפולה שלמה של \( n \), כלומר ש-\( \frac{k}{n} \) הוא שלם. במילים אחרות, הגרעין יהיה \( \mathbb{Z} \) ולכן קיבלנו ש-\( \mathbb{Q}/\mathbb{Z} \) איזומורפי לחבורת שורשי היחידה. זו חבורה מאוד מעניינת: מצד אחד, לא נוצרת סופית. מצד שני, בת-מניה, וכל איבר בה הוא כן מסדר סופי.

אפשר לעבור לרציונליים עם כפל. צריך להעיף את 0 מהקבוצה, אבל פרט לכך שאר האיברים נשארים, ואת הקבוצה שמקבלים מסמנים ב-\( \mathbb{Q}^{*} \). בבירור החבורה הזו לא איזומורפית ל-\( \mathbb{Q} \), כי פרט ל-1 ולמינוס 1 כל האיברים בה הם מסדר אינסופי (והנה נימוק ישיר יותר: נניח שהן כן איזומורפיות אז יש ב-\( \mathbb{Q} \) איבר \( a \) שעובר אל \( 2 \) ב-\( \mathbb{Q}^{*} \); אז \( \frac{a}{2} \) היה חייב לעבור אל \( \sqrt{2} \) שכלל איננו רציונלי). מה היא כן? זו חבורה שנוצרת על ידי מספר בן מניה של יוצרים שונים - המספרים הראשוניים, ועוד \( -1 \) שמאפשר לנו לקבל את השלמים. כלומר, \( \mathbb{Q}^{*}\cong\mathbb{Z}_{2}\oplus\mathbb{Z}\oplus\mathbb{Z}\oplus\dots \). שימו לב שכאן לא השתמשתי במכפלה ישרה אלא בסכום ישר, כי כל מספר רציונלי הוא מכפלה של מספר סופי של חזקות של ראשוניים - או, לחילופין, של כל אינסוף הראשוניים אבל כשהחזקה של כולם פרט למספר סופי היא 0. אם רוצים להיפטר מה-\( \mathbb{Z}_{2} \) המעצבן בהתחלה אפשר להסתכל רק על הרציונליים החיוביים: \( \mathbb{Q}^{+}\cong\mathbb{Z}\oplus\mathbb{Z}\oplus\dots \) - זה נותן לנו אינטואיציה טובה לגבי הסכום הישר של כל החבורות הציקליות האינסופיות.

בואו נעבור לממשיים. יש שתי חבורות מתבקשות כשמדברים על הממשיים: \( \left(\mathbb{R},+\right) \) של כל הממשיים עם החיבור, ו-\( \left(\mathbb{R}^{*},\cdot\right) \) של כל הממשיים פרט לאפס עם הכפל. כמו עם הרציונליים, \( \mathbb{R}^{*}\cong\mathbb{Z}_{2}\times\mathbb{R}^{+} \) כאשר \( \mathbb{R}^{+} \) הם הממשיים החיוביים עם כפל, ועכשיו קל לראות ש-\( \left(\mathbb{R},+\right)\cong\left(\mathbb{R}^{+},\cdot\right) \) עם ההומומורפיזם \( x\mapsto e^{x} \), כי הרי \( e^{x+y}=e^{x}\cdot e^{y} \). ומה עם \( \mathbb{R}/\mathbb{Z} \)? באופן יבש, זו החבורה של כל המספרים בקטע החצי פתוח \( [0,1( \) עם פעולת חיבור מודולו 1 (למשל, \( 0.5+0.75=0.25 \)). אבל אני מעדיף לראות את החבורה הזו בתור מעגל היחידה באופן הבא: נגדיר הומומורפיזם מ-\( \mathbb{R} \) אל החבורה \( \mathbb{C} \) עם הפעולה הרגילה של כפל מרוכבים על ידי \( x\mapsto\left(\cos2\pi x,\sin2\pi x\right) \) (כלומר, \( x \) הולך אל המספר המרוכב \( e^{i2\pi x} \)). הגרעין שלו הוא בדיוק ה-\( x \)-ים שעבורם \( \cos2\pi x=1 \) ו-\( \sin2\pi x=0 \), כלומר ש-\( x\in\mathbb{Z} \).

הדוגמא הבאה היא פונקציות. הרכבת פונקציות היא לא קומוטטיבית ולכן לא נקבל כך חבורות אבליות, אבל אפשר לבצע חיבור וכפל נקודתיים של פונקציות. למשל, אפשר לדבר על חבורת כל הפונקציות \( f:\mathbb{R\to\mathbb{R}} \) עם פעולת חיבור נקודתית, כלומר \( \left(f+g\right)\left(x\right)=f\left(x\right)+g\left(x\right) \) . זו בוודאי חבורה ואיבר היחידה הוא פונקציית האפס. אפשר גם לדבר על אותו דבר עם כפל נקודתי, אבל אז צריך לדרוש שהפונקציות שלנו לא יתאפסו באף נקודה. אפשר גם לדבר על פונקציות רציפות, וכדומה.

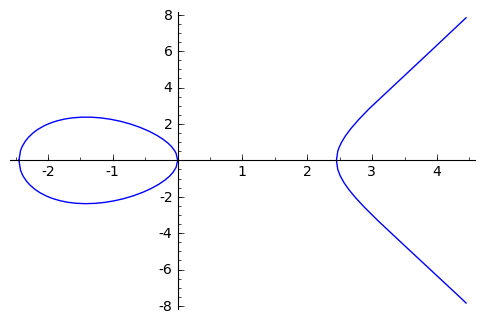
ואני רוצה לסיים עם אזכור של חבורות אבליות מפורסמות למדי: עקומים אליפטיים. בנפנוף ידיים קל (כי יש הגדרות כלליות יותר), עקום אליפטי הוא אוסף כל הפתרונות של משוואה מהצורה \( y^{2}=x^{3}+ax+b \) (עם עוד דרישה על הפרמטרים שלא אציג כרגע). הנה תמונה של עקום טיפוסי:

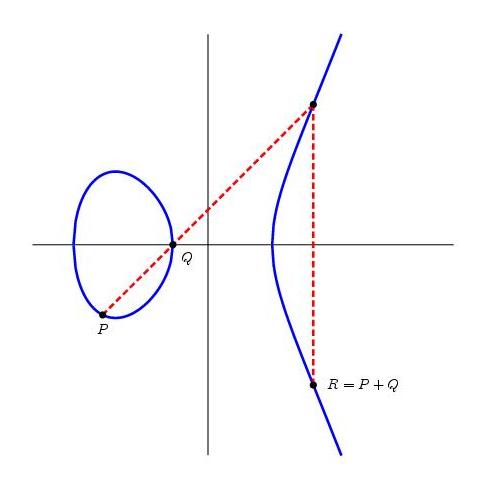
ליצור הזה מוסיפים עוד נקודה אחת “באינסוף” שתשתמש בתור איבר יחידה, ומקנים לו מבנה של חבורה בצורה המוזרה-לכאורה הבאה: חיבור של שתי נקודות פירושו לקחת את הישר שעובר דרכן, ואם הוא חותך את העקום - לשקף את נקודת החיתוך ביחס לציר \( x \) וזו תהיה התוצאה. אם הישר לא חותך את העקום, אז התוצאה היא הנקודה “באינסוף”. מתברר שעם ההגדרה הזו מקבלים חבורה אבלית. מאיפה ההגדרה הזו הגיעה? יש דרכים יפות להגיע אליה אבל אני לא אכנס לזה כרגע.

העניין הוא שקצת הסתרתי מכם פרטים. אמרתי “אוסף כל הפתרונות של משוואה מהצורה כך-וכך”, אבל לא אמרתי מאיפה אפשר לקחת את הפתרונות. אפשר לדבר, למשל, על אוסף כל הפתרונות של המשוואה מעל המרוכבים. במקרה הזה אפשר להוכיח שהחבורה שנקבל איזומורפית לטורוס. אפשר לדבר על הפתרונות מעל הממשיים, או מעל הרציונליים (החקירה של הפתרונות הרציונליים של עקומים אליפטיים היא תחום מרתק; היא מתקשרת, למשל, להוכחת המשפט האחרון של פרמה). אפשר גם לדבר על הפתרונות מעל שדות סופיים (מושג שטרם הגדרתי בסדרת הפוסטים הזו, אבל תחשבו על \( \mathbb{Z}_{p} \) עם פעולות חיבור וכפל; זו דוגמה פשוטה). במקרה האחרון נקבל חבורות סופיות, כי יש רק מספר סופי של פתרונות. הופה! חבורה אבלית סופית? אנחנו כבר יודעים בדיוק איך היא נראית, יש לנו את משפט המיון!

ובכן… זה מחזיר אותי למשהו שאמרתי באחד מהפוסטים הקודמים, על כך שלא מספיק לדעת ששתי חבורות הן איזומורפיות; צריך גם לדעת איך הן איזומורפיות. יש שיטות הצפנה שמתבססות על עקומים אליפטיים שבהם הרעיון הוא בדיוק שבגלל שהייצוג של החבורה האבלית ה”פשוטה” שלנו הוא באמצעות עקום אליפטי, קשה לבצע בה פעולות חשבון שהיו טריוויאליות אם היה לנו את הייצוג של החבורה הזו בתור \( \mathbb{Z}_{n} \), למשל. אני מקווה לתאר את הדברים הללו בעתיד, אבל בסדרת הפוסטים הזו אני חושב שאעבור לדבר על חבורות לא אבליות.