אז מהי PSPACE?
שני המשאבים המרכזיים שמדברים עליהם בתורת הסיבוכיות הם זמן וזכרון. בכל הנוגע לזמן, הפורמליסטיקה בוחרת להגדיר “זמן יעיל” כזמן שהוא פולינומי בגודל הקלט של האלגוריתם - כלומר, אם \( x \) הוא הקלט וב-\( \left|x\right| \) אנחנו מסמנים את אורכו (מספר הביטים שמקודדים אותו), אז אלגוריתם הוא “יעיל” בכל הנוגע לזמן הריצה אם קיים פולינום \( p \) כך שלכל \( x \), זמן הריצה של האלגוריתם על \( x \) אינו עולה על \( p\left(\left|x\right|\right) \). זו בחירה שנראית מוזרה למדי במבט ראשון - זמן ריצה של \( n^{1000} \) הוא ממש לא מה שהיינו חושבים עליו בתור יעיל מלכתחילה, בפרט בהתחשב בכך שבעולם מדעי המחשב נעשים מאמצים לא מבוטלים לרדת מזמן כמו \( n^{3} \) אל \( n^{2} \).
אבל תורת הסיבוכיות מתעניינת בחסמים תחתונים. היא רוצה להראות שבעיות מסויימות הן קשות. כל כך קשות, שלא משנה כמה נרשה לפולינום להיות גדול, עדיין לא יהיה ניתן לפתור אותן בזמן פולינומי. הוכחה ש-\( \mbox{P}\ne\mbox{NP} \) תראה כי אלפי בעיות שצצות ועולות בכל תחומי מדעי המחשב הן אכן קשות במובן הזה. כך שה”ויתור” שאנחנו מבצעים בכך שאנו מרשים לזמן הריצה להיות פולינום גדול מאוד אינו מהותי; רק חשוב לזכור ששייכות ל-\( \mbox{P} \) עדיין אינה אומרת שקיים פתרון טוב לבעיה. יש לבחירה בפולינומים דווקא גם סיבות טובות נוספות ובראשן הרצון להימנע מהתלות של סיבוכיות זמן הריצה במודל החישוב הספציפי שאנו בוחרים לעבוד איתו, אך נעזוב את זה לבינתיים.
כשאנו באים לדבר על סיבוכיות זכרון, נראה טבעי לגמרי לנקוט באותה הגדרה בדיוק - זכרון “יעיל” הוא זכרון שהוא פולינומי בגודל הקלט. למחלקה המתאימה קוראים \( \mbox{PSPACE} \), ובפוסט הזה ננסה להבין איך בדיוק היא נראית ומתנהגת ביחס לשאר מחלקות הסיבוכיות. נתחיל מהשורה התחתונה - \( \mbox{PSPACE} \) היא מחלקה ענקית. היא כוללת את רוב העולם ה”מעניין”. הגדרות יותר זהירות של סיבוכיות זכרון עשויות להצביע על כך שעדיף לדבר על מחלקות של זכרון לוגריתמי, דוגמת \( \mbox{NL} \) שהוזכרה בפוסט על משפט אימרמן; אבל זה לא אומר ש-\( \mbox{PSPACE} \) היא לא מחלקה מעניינת לכשעצמה, גם אם קשה להגיד שהיא ממדלת חישובים “יעילים”.
האבחנה הראשונה היא ש-\( \mbox{P}\subseteq\mbox{PSPACE} \), מהטעם הפשוט שכדי “לבזבז” זכרון, צריך לבזבז זמן על הגישה אליו. אם הולכים להגדרה הפורמלית על ידי מכונת טיורינג, זמן חישוב מוגדר כמספר הצעדים שמכונת הטיורינג מבצעת, ואילו הזכרון שהיא השתמשה בו מוגדר בתור אינדקס התא הרחוק ביותר שהראש שלה הגיע אליו - וכדי להגיע למרחק כזה, צריך לבצע צעדים, וזה גוזל זמן. אם כל הזמן שאפשר לבזבז הוא פולינומי, אי אפשר לבזבז יותר מאשר זכרון פולינומי. הגיון סביר (כל עוד לא עובדים עם מודלים מוזרים שבהם אפשר לגשת לכמות עצומה של זכרון בכל צעד חישוב).
מכיוון שאמרתי ש-\( \mbox{PSPACE} \) היא מחלקה ענקית ומפחידה, מתבקש להאמין לי ולהגיע למסקנה ש-\( \mbox{P}\ne\mbox{PSPACE} \), אך כאן אנו נתקלים באכזבה רבתי - אין שום הוכחה כיום לכך ש-\( \mbox{P}\ne\mbox{PSPACE} \), אף שעולם מדעי המחשב התיאורטיים יוכה בתדהמה אם יתברר ש-\( \mbox{P=PSPACE} \), ותדהמה גדולה משמעותית מהתדהמה ש-\( \mbox{P}=\mbox{NP} \) יגרום לה. למעשה, אם יתברר כי \( \mbox{P=PSPACE} \) כל מחלקות הסיבוכיות שאני עומד לדבר עליהן בהמשך הפוסט יהיו מיותרות לחלוטין כי כולן יהיו שוות ל-\( \mbox{P} \). זה מאוד, מאוד לא סביר; העובדה שעוד אין הוכחה ש-\( \mbox{P\ensuremath{\ne}PSPACE} \) רק מעידה עד כמה מדעי המחשב התיאורטיים עדיין בחיתוליהם.
בשביל חימום, בואו נדבר על \( \mbox{NP} \). ההגדרה שאני אוהב ל-\( \mbox{NP} \) מדברת על שפות שיש “עדים” לשייכות מילים אליהן. פורמלית, יש אלגוריתם “מוודא” פולינומי \( V \) שמקבל זוג \( \left(w,\pi\right) \), ועונה כן או לא, כך שאם \( w\in L \) קיים \( \pi \) כך ש-\( V \) מקבל את \( \left(w,\pi\right) \), ואם \( w\notin L \) אז לכל \( \pi \) שלא יהיה, \( V \) ידחה את \( \left(w,\pi\right) \). המגבלה היחידה על \( \pi \) היא שיהיה פולינומי בגודלו ביחס ל-\( w \), אחרת \( V \) ממילא לא יוכל לקרוא את כולו.
מכונת \( \mbox{PSPACE} \) עבור \( L\in\mbox{NP} \) תשתמש בכוח הגס האלים והברוטלי ביותר שיש: בהינתן \( w \), היא תעבור סדרתית על כל הזוגות \( \left(w,\pi\right) \) עבור \( \pi \) שאינו גדול מדי (לא חורג מהחסם הפולינומי שמאפיין את \( L \)), ולכל אחד מהם היא תריץ את \( V \) על \( \left(w,\pi\right) \) ותקבל רק אם \( V \) מקבל מתישהו. מכיוון ש-\( V \) פולינומי בזמן, הסימולציה שלו דורשת זכרון פולינומי, ואת המקום הזה אפשר למחזר בין הרצות שונות. זה גורם לכך שכל האלגוריתם הזה, למרות שהוא עובר על מספר אקספוננציאלי של \( \pi \)-ים שיש לבדוק, דורש רק זכרון פולינומי, ומכריע את אותה השפה. זה מראה ש-\( \mbox{NP}\subseteq\mbox{PSPACE} \) (ולכן אם \( \mbox{P=PSPACE} \) זה גם גורר מיידית ש-\( \mbox{P=NP} \)).
הגישה האלימה הזו - פשוט לעבור על כל האפשרויות וזו לא בעיה כי כל אפשרות בפני עצמה צורכת מעט זכרון ואפשר למחזר - עובדת שוב ושוב עבור מחלקות סיבוכיות שונות ומשונות. כך למשל קחו את \( \mbox{BPP} \) - המחלקה של חישובים הסתברותיים יעילים. לא ברור הקשר שלה ל-\( \mbox{NP} \) (בפרט לא ברור אם אחת מהמחלקות מכילה את השניה), אבל חיפוש ממצה מוחץ כמו זה שנעשה עבור \( \mbox{NP} \) מראה גם ש-\( \mbox{BPP}\subseteq\mbox{PSPACE} \). ומה עם חישובים קוונטיים? המחלקה הרלוונטית של חישובים קוונטיים יעילים נקראת \( \mbox{BQP} \). יש תקווה גדולה ש-\( \mbox{P}\ne\mbox{BQP} \) ולכן חישובים קוונטיים (שאולי יהיה ניתן לממש יום אחד במציאות) מסוגלים לעשות יותר משחישובים רגילים מסוגלים; אבל יש לכל העניין הזה גבול - אפשר להראות גם ש-\( \mbox{BQP}\subseteq\mbox{PSPACE} \) (ולכן אם יתגלה ש-\( \mbox{P=PSPACE} \) בפרט זה יוכיח שחישובים קוונטיים אינם יעילים יותר מחישובים קלאסיים - מתחילים להבין למה כל זה נתפס כ”לא סביר”?)
את \( \mbox{NP} \) אפשר להכליל באופן הבא: אם אפשר לתאר כל שפה ב-\( \mbox{NP} \) בתור \( L=\left\{ x|\exists y:\left(x,y\right)\in S\right\} \) כאשר \( S \) הוא יחס כלשהו שניתן לזהות בזמן פולינומי, אפשר גם לדבר על שפות שאפשר לתאר, למשל, על ידי \( L=\left\{ x|\exists y_{1}\forall y_{2}\exists y_{3}\forall y_{4}:\left(x,y_{1},y_{2},y_{3},y_{4}\right)\in S\right\} \). המשחק הזה של הכמתים - מעבר מ”קיים” ל”לכל” וכן הלאה - מוסיף כוח חישובי כאשר מגדירים שפות ללא מגבלות סיבוכיות (כלומר, דורשים רק ש-\( S \) תהיה ניתנת לזיהוי, לא בהכרח בזמן פולינומי). כאשר אנחנו עוברים לעולם הפולינומי, לא ידוע לנו אם אכן כל החלפת כמתים מוסיפה כוח, אבל ההשערה היא שאכן כך המצב. ב-\( \Sigma_{n}^{p} \) מסמנים את כל השפות שאפשר לתאר בצורה כזו עם \( n \) חילופי כמתים (כך למשל \( \mbox{NP}=\Sigma_{1}^{p} \). לאוסף המחלקות \( \Sigma_{n}^{p} \) שמתקבל כך קוראים ההירכייה הפולינומית, ואת האיחוד של כולן מסמנים ב-\( \mbox{PH} \).
ההיררכייה הפולינומית היא עולם מרתק שראוי בהחלט לפוסט נפרד. כאן תיארתי אותה רק בשביל לתאר את הכוח של \( \mbox{PSPACE} \). כן, ניחשתם נכון - כל ההיררכייה מוכלת בתוך \( \mbox{PSPACE} \). שוב, פתרון הכוח הגס עובד כאן.
בואו נעבור לדבר על משהו שונה לגמרי - משחקים. המשחקים שארצה לדבר עליהם כאן הם משחקים לשני שחקנים עם ידיעה שלמה - כלומר, אין הגרלות (להבדיל ממשחקי קלפים, למשל) ואין מידע שהשחקנים מחביאים זה מזה (כמו ב”צוללות” - שם אין הגרלות, אבל אף שחקן לא יודע איפה הצוללות של השחקן השני). אפשר לדבר גם על משחקים בלי ידיעה שלמה אבל בואו נעזוב את זה לבינתיים. בואו גם נניח לצורך פשטות שתוצאת תיקו אינה אפשרית במשחקים הללו. בפוסט הקודם שעסק במשחק נים ראינו בדיוק דוגמה למשחק שכזה.
כעת, משפט צרמלו (שהזכרתי בעבר וגם בפוסט הקודם) קובע שבמשחק כזה תמיד יש לאחד השחקנים אסטרטגיית ניצחון - דרך פעולה שתבטיח לו ניצחון בלי תלות במה שעושה השחקן השני. הדרך להוכיח זאת היא באמצעות עץ המשחק - עץ שצמתיו הם עמדות במשחק, והבנים של כל צומת הם העמדות שאפשר להגיע אליהן על ידי ביצוע מהלך על ידי השחקן שכרגע תורו. את העלים בעץ מסמנים ב-1 או 0, כאשר 1 מסמן ניצחון עבור אליס, ו-0 הפסד עבור אליס, ולכן ניצחון עבור בוב (אליס ובוב הם השמות שאני נותן לשחקנים). כעת ניתן סימון לשאר הצמתים בעץ בדרך הבאה: אם כל הבנים של צומת כבר מסומנים, ואם בצומת הזה תורה של אליס לשחק, אז נסמן אותה ב-1 אם ולו אחד מהבנים מסומן ב-1, ואחרת נסמן ב-0. אם תורו של בוב לשחק, אז נסמן ב-0 אם ולו אחד מהבנים מסומן ב-0, ואחרת נסמן ב-1. כעת כל שנותר לעשות הוא לבדוק באיזה מספר סומן השורש של העץ כדי לדעת למי יש אסטרטגיית ניצחון במשחק. נסו להבהיר לעצמכם למה זה עובד.
שימו לב שההוכחה הזו קונסטרוקטיבית לגמרי - היא נותנת אלגוריתם, ואלגוריתם פשוט למדי, שבהינתן משחק מאפשר לחשב את אסטרטגיית הניצחון בו. רק צריך להיות מסוגלים לייצג באופן יעיל את עץ המשחק ולטייל עליו. האלגוריתם הפשוט ביותר לסריקת גרפים - חיפוש לעומק, DFS - עובד כאן. סיבוכיות הזכרון של האלגוריתם הזה היא כעומק העץ כפול כמות הזכרון שנדרשת כדי לייצג צומת; המסקנה היא שאם כל צומת ניתנת לייצוג בזכרון פולינומי (פולינומי ביחס למה? לפרמטר כלשהו של המשחק) והאורך המקסימלי של משחק הוא מספר פולינומי של צעדים, אז הבעיה של הכרעה למי יש אסטרטגיית ניצחון במשחק היא - ניחשתם נכון, ב-\( \mbox{PSPACE} \).
עבור משחק כמו נים המהומה הזו לא הכרחית - ראינו בפוסט הקודם שקל מאוד להכריע (בזמן פולינומי) עבור עמדה במשחק למי יש אסטרטגיית ניצחון. אבל הנה משחק קשה יותר - גאוגרפיה. במשחק המטופש הזה כל שחקן אומר שם של עיר, והשחקן השני צריך להגיד עיר חדשה, שהאות הראשונה בה היא האות האחרונה בשם העיר הקודמת. מפסיד מי שלא יודע איך להמשיך. המשחק הזה לא קשה כל כך, אבל יש לו הכללה רחבה למדי - “גאוגרפיה מוכללת”, Generalized Geography. במשחק הזה נתון גרף מכוון. מתחילים מאיזו צומת, ובכל סיבוב אחד השחקנים בוחר צומת שכנה ועובר אליה. אסור לחזור לאותה צומת פעמיים, ומפסיד מי שלא יכול לנוע עוד. איך זה קשור לגאוגרפיה המקורית? הנה תרגיל - נסו למדל את גאוגרפיה בתור משחק בגאוגרפיה-מוכללת. זה לא קשה במיוחד.
מקרה פרטי נחמד של גאוגרפיה מוכללת היא זו: על לוח שחמט שמים מלך (לא משנה איפה), ועכשיו כל אחד מהשחקנים מזיז אותו בתורו, תחת האילוצים שאסור להיכנס פעמיים לאותה משבצת, וגם אסור לנוע באלכסון (כלומר, זה לא בדיוק מלך אלא מלך נכה). כאן אפשר להוכיח מייד שלשחקן שמתחיל יש אסטרטגיית נצחון וההכללה למחלקה רחבה יותר של משחקים נובעת מאליה (רמז עבה לבקיאים בגרפים: שידוך).
בגאוגרפיה מוכללת הקלט הוא הגרף (והצומת שמתחילים בו, אם כי זה פחות קריטי), ומכיוון שבבירור אורך המשחק הוא פולינומי (כי בכל צעד שורפים צומת בגרף) אז הכרעה למי יש אסטרטגיית נצחון במשחק היא ב-\( \mbox{PSPACE} \). זה כנראה כבר לא מפתיע אתכם בשלב הזה; ההפתעה האמיתית היא שהבעיה הזו היא במובן מאוד קונקרטי “הבעיה הכי קשה ב-\( \mbox{PSPACE} \)” - זו בעיה שמאפיינת באופן מושלם למדי את הרעיון של \( \mbox{PSPACE} \). בניסוח קצת יותר פורמלי - זוהי בעיה \( \mbox{PSPACE} \)-שלמה, באותו אופן שבו בעיות כמו \( \mbox{SAT} \) או מעגל המילטוני או 3-צביעה של גרפים הן \( \mbox{NP} \)-שלמות. פורמלית זה אומר שאם נתונה שפה כלשהי - כלשהי ששייכת ל-\( \mbox{PSPACE} \), אז אפשר להמיר כל קלט למשחק גאוגרפיה מוכללת, כך שאם הקלט המקורי היה שייך לשפה, אז במשחק המתקבל ממנו יהיה מהלך נצחון ללבן, ואם הוא לא היה שייך לשפה, אז במשחק המתקבל ממנו יהיה מהלך ניצחון לשחור.
איך מוכיחים את זה? ובכן, בעקיפין. כמו שאף אחד לא מוכיח באופן ישיר ש-3-צביעה היא בעיה \( \mbox{NP} \)-שלמה, כך גם כאן - יש בעיה “קנונית” שיחסית קל להוכיח עבורה באופן ישיר שהיא \( \mbox{PSPACE} \)-שלמה, וכדי להראות שבעיות אחרות דוגמת \( \mbox{GG} \) הן \( \mbox{PSPACE} \)-שלמות, פשוט מראים איך פותרים את אותה בעיה קנונית באמצעותן. השפה הקנונית עבור \( \mbox{PSPACE} \) נקראת \( \mbox{TQBF} \) - ראשי תיבות של True Quantified Boolean Formulas.
נוסחה בוליאנית מורכבת ממשתנים שיכולים לקבל “אמת” ו”שקר” - \( \mbox{T} \) ו-\( \mbox{F} \) - ומחוברים ביניהם עם “וגם” (\( \wedge \)), “או” (\( \vee \)) ו”לא” (\( \neg \)). למשל, \( \left(x_{1}\vee x_{2}\right)\wedge\left(\neg x_{1}\vee\neg x_{2}\right) \) היא נוסחה שמקבלת ערך אמת רק אם מציבים ערך אמת לאחד מהמשתנים וערך שקר לשני (זו דרך לתאר את פונקציית ה-XOR באמצעות \( \wedge,\vee,\neg \)). השפה \( \mbox{SAT} \) שהזכרתי קודם מורכבת מאוסף כל הנוסחאות הללו שהן ספיקות - כלומר, שיש השמה שמספקת אותן. \( \mbox{TQBF} \) היא הכללה כלשהי של העסק: אם \( \varphi\left(x_{1},\dots,x_{n}\right) \) היא נוסחה בוליאנית כלשהי במשתנים \( x_{1},\dots,x_{n} \), אז פסוק ה-\( \mbox{QBF} \) המתאים הוא פסוק מהצורה \( \exists x_{1}\forall x_{2}\dots\exists x_{n}\varphi\left(x_{1},\dots,x_{n}\right) \). כלומר, פסוק שאומר “קיימת השמה ל-\( x_{1} \) כך שלכל השמה ל-\( x_{2} \) קיימת השמה ל-\( x_{3} \)… קיימת השמה ל-\( x_{n} \) כך ש-\( \varphi \) מקבל ערך אמת תחת ההשמה הזו”. ה”לכל” הוא בדיוק מה שמסבך את העניינים כאן, וכמו שאמרתי קודם על ההיררכייה הפולינומית, הפינג-פונג הזה בין “לכל” ו”קיים” מגדיל עוד ועוד את כושר הביטוי של הפסוקים הללו. שימו לב שבניגוד לפסוקי \( \mbox{SAT} \) חסרי הכמתים, כאן לפסוק יש ערך אמת מוגדר - הוא או נכון או לא נכון.
\( \mbox{TQBF} \) היא בדיוק שפת כל הפסוקים המכומתים שערך האמת שלהם הוא \( \mbox{T} \). הבדל מהותי בינה לבין שפות שמופיעות בהיררכייה הפולינומית הוא שאין מגבלה על מספר ההחלפות של כמתים - בתוך \( \mbox{TQBF} \) אפשר למצוא פסוקים שבהם יש 100 החלפות, או זיליארד, או \( 10^{100^{100^{100}}} \) וכל מה שתרצו. וכפי שודאי כבר ניחשתם, קל מאוד להראות ש-\( \mbox{TQBF} \) שייכת ל-\( \mbox{PSPACE} \) על ידי אותם שיקולי כוח גס שכבר דיברנו עליהם. הפאנץ’ הוא שזהו סוף הדרך - \( \mbox{TQBF} \) היא שפה \( \mbox{PSPACE} \)-שלמה, ולכן “הקשה ביותר” ב-\( \mbox{PSPACE} \) (כפי שכבר הבנתם, התואר הזה לא מוחזק על ידי שפה יחידה; גם \( \mbox{GG} \) מחזיקה בו). במובן מסויים, \( \mbox{TQBF} \) היא משחק מאורך פולינומי בצורתו המזוקקת ביותר: בתור הראשון, השחקן הלבן בוחר ערך (\( \mbox{T} \) או \( \mbox{F} \)) למשתנה הראשון; בתור השני השחור בוחר ערך למשתנה השני; וכן הלאה. בסוף המשחק (כשנגמרים המשתנים) מחשבים את ערך האמת של \( \varphi \) ובודקים מי ניצח.
למה \( \mbox{TQBF} \) היא \( \mbox{PSPACE} \)-שלמה? זה שייך לפוסט נפרד. ההוכחה היא יפה ומחוכמת, גם אם לא מסובכת במיוחד. את הפוסט הזה אני רוצה לסיים בשכנוע ש-\( \mbox{GG} \) קשה לפחות כמו \( \mbox{TQBF} \), כלומר להראות איך אפשר לתרגם פסוק \( \mbox{TQBF} \) כללי לגרף שעליו משחקים \( \mbox{GG} \).
ראשית, אפשר להגביל קצת את \( \mbox{TQBF} \) ולדרוש ש-\( \varphi \) יהיה \( \mbox{CNF} \) - פסוק שהוא \( \wedge \) של פסוקיות שכל אחת מהן היא \( \vee \) של ליטרלים (ליטרל הוא משתנה או שלילה של משתנה) השמה מספקת פסוק \( \varphi \) שכזה רק אם בכל פסוקית, יש לפחות ליטרל אחד שמקבל \( \mbox{T} \). באופן שקול ומסובך יותר (אבל יש סיבה שאני מציין אותו), השמה מספקת פסוק \( \varphi \) אם לא ניתן למצוא פסוקית שבה אף אחד מהמשתנים לא קיבל \( \mbox{T} \) בהשמה. נניח גם שהכמת האחרון בפסוק ה-\( \mbox{TQBF} \) הוא תמיד \( \exists \), כלומר יש מספר אי זוגי של משתנים (למעשה, זו הייתה הצורה הכללית של הפסוקים שהצגתי קודם - כמה מכם שאלו את עצמם “רגע, האם אפשר שסדרת הכמתים תסתיים גם ב-\( \forall \)”?).
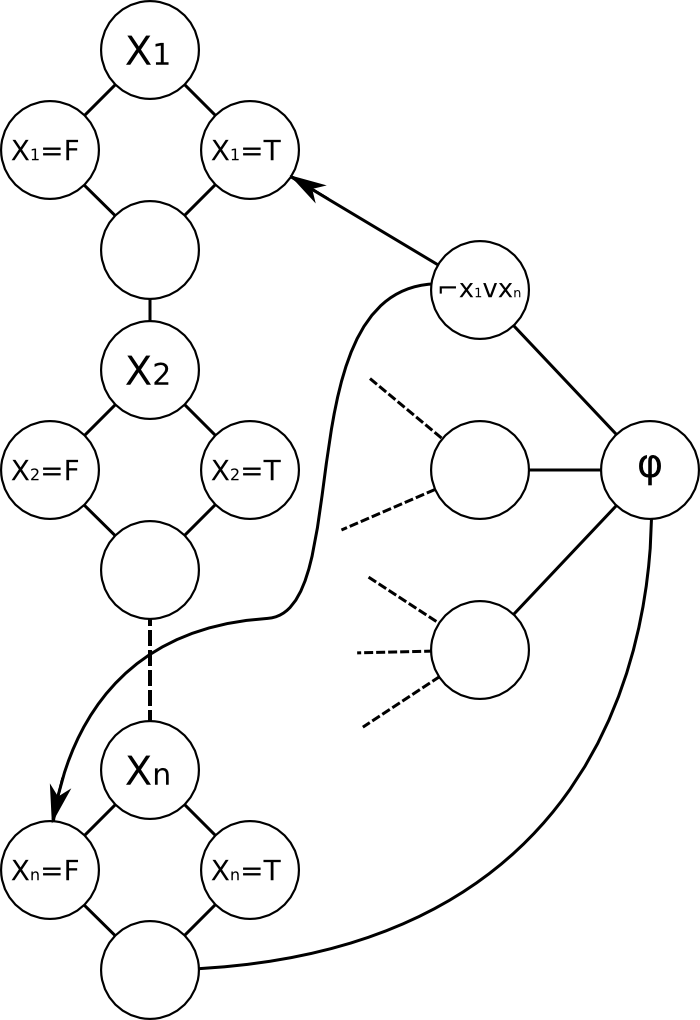
כעת, הגרף שעליו ישחקו את ה-\( \mbox{GG} \) (בהינתן פסוק ה-\( \mbox{TQBF} \) שהוא אמור לסמלץ) יהיה בנוי משני רכיבים - הראשון מסמלץ את השלב שבו השחקנים בוחרים השמה למשתנים של \( \varphi \), והשני יסמלץ נסיון של השחקן השני להראות לשחקן הראשון ש-\( \varphi \) לא סופק, כלומר להציג בפני השחקן הראשון פסוקית ב-\( \varphi \) שהשחקן הראשון, לכאורה, לא יכול לספק. כרגיל, תמונה אחת שווה אלף מילים אז הנה איך הגרף נראה, ואנסה גם להסביר קצת מה הולך פה במילים:
הרכיב הראשון (השמאלי) מסמלץ את הבחירות באופן הבא: לכל משתנה \( x_{i} \) יש צומת. מהצומת הזה יוצאות שתי קשתות, אל צמתים שמסומנים ב-\( x_{i}=\mbox{F} \) ו-\( x_{i}=\mbox{T} \). הבחירה של השחקן לאיזה משני הצמתים ללכת תתורגם, בסופו של דבר, להשמה למשתנה \( x_{i} \).
אחרי שמסתיים המשחק בחלק הראשון, עוברים בחלק השני לתת-גרף שבו יש צומת לכל פסוקית של \( \varphi \). השחקן השני בוחר לאיזה מהצמתים הללו ללכת. כעת, אם בפסוקית הזו מופיע המשתנה \( x_{i} \), אז תהיה קשת מהצומת של הפסוקית אל הצומת \( x_{i}=\mbox{F} \), ואילו אם יש בה את \( \neg x_{i} \), תהיה קשת ממנה אל \( x_{i}=\mbox{T} \). זה אולי נראה לכם הפוך ממה שאמור להיות, וזה לא מקרי - הנקודה היא שאם בחלק הראשון של המשחק נבחר, למשל \( x_{i}=\mbox{T} \), אז הצומת הזה “שרוף” ואי אפשר להיכנס אליו שוב. את הכניסה לצומת \( x_{i}=\mbox{F} \) מתוך הצומת של הפסוקית שמכילה את \( x_{i} \) צריך לראות לא בתור בחירה של \( \mbox{F} \) עבור \( x_{i} \), כי כבר בחרנו ש-\( x_{i}=\mbox{T} \) בתחילת המשחק; צריך לראות אותה בתור כניסה לצומת פנוי ותו לא. מכיוון שהצומת פנוי, שחקן 1 שרד את הסיבוב הזה - ושחקן 2 הפסיד, כי הצומת שאליו חייבים להיכנס אחרי \( x_{i}=\mbox{F} \) כבר נשרף. במילים אחרות, אם לכל צומת פסוקית ששחקן 2 יבחר, שחקן 1 יכול להמשיך לבצע עוד צעד אחד במשחק (והוא יכול רק אם הפסוקית הזו הסתפקה על ידי ליטרל כלשהו), אז שחקן 2 הפסיד, ואחרת הוא ניצח.
עם הרדוקציה הזו מגיע הזמן לסיים את הפוסט. לא שהתחלתי אפילו לספר את כל הדברים המעניינים שיש לספר על \( \mbox{PSPACE} \), אבל אני מקווה שלפחות נתתי תחושה כלשהי של מה זה בכלל; ובפרט, הצגתי את \( \mbox{TQBF} \) שהולכת להיות השחקנית החשובה בהמשך.
נהניתם? התעניינתם? אם תרצו, אתם מוזמנים לתת טיפ: