הדרך מהאקספוננט לטריגונומטריה רצופה משוואות דיפרנציאליות מסדר שני

בפוסט הקודם עסקתי באופן שבו פונקציית האקספוננט, \( e^{x} \), “צצה באופן טבעי” בתור פתרון המשוואה הדיפרנציאלית \( f^{\prime}=f \) עם תנאי ההתחלה \( f\left(0\right)=1 \). כעת אני רוצה להרחיב קצת יותר על פתרון משוואות דיפרנציאליות, כשהיעד הסופי הוא הגעה למשוואות שפתרונן דורש סינוסים וקוסינוסים (כפי שנראה, משוואות כאלו קשורות בקשר הדוק לפונקצית האקספוננט), ובכך לקבל מוטיבציה לא גאומטרית להגדרתן. ראשית אפרע חוב מהפוסט הקודם - אמרתי שפתרון המשוואה \( f^{\prime}=f \) ייתן לנו “קרש קפיצה” לפתרון משוואות אחרות - כעת אוכל להסביר מעט יותר למה התכוונתי.

הבה נסבך מעט את המשוואה הזו - נניח כי כעת היא \( f^{\prime}=a\cdot f \). האם אנו יודעים לפתור אותה? האינטואיציה אומרת לנסות ולהשתמש בפונקציה דומה ל-\( e^{x} \) שאותה מצאנו קודם, ולא צריך לחפש יותר מדי: \( e^{ax} \) היא פונקציה שפותרת את המשוואה הזו, ולכן פתרון כללי למשוואה הזו הוא מהצורה \( \lambda e^{ax} \), כש-\( \lambda \) נקבע על פי תנאי ההתחלה של המשוואה (כזכור, אחרי שקבענו תנאי התחלה למשוואה, דהיינו ערך ש-\( f \) מקבלת בנקודה כלשהי, נובע ש-\( \lambda e^{ax} \) הוא הפתרון היחיד למשוואה).

האקשן האמיתי מתחיל כשמגיעים למשוואות מהצורה \( f^{\prime}=a\left(x\right)f+b\left(x\right) \), כלומר כאלו שבהן המקדם של \( f \) הוא פונקציה שבעצמה תלויה ב-\( x \), ושיש בהן גם מקדם “חופשי” שגם הוא יכול להיות פונקציה כלשהי שתלויה ב-\( x \). כדי להתמודד עם משוואות כאלו כבר צריך לדעת לעשות אינטגרלים ויש מהומות, ולא אכנס לזה כעת (בסופו של דבר, אני לא מנסה כרגע להיות ספר לימוד במשוואות דיפרנציאליות). תחת זאת אעבור למשוואות מסדר שני, ואעשה זאת בעזרת מוטיבציה פיזיקלית שכבר הזכרתי לא מזמן - תנועה הרמונית פשוטה.

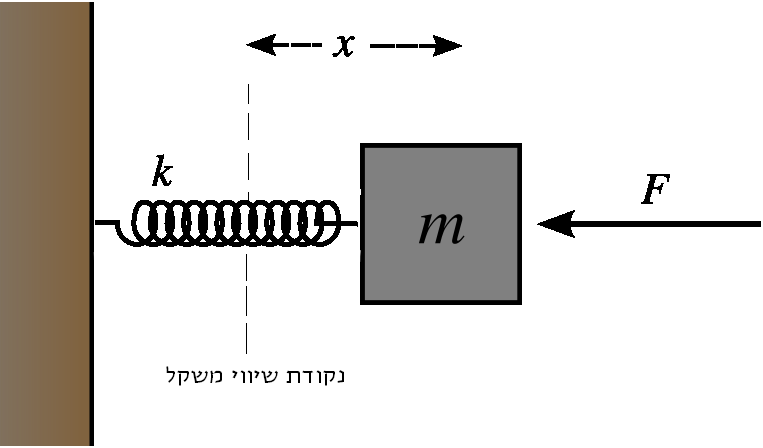
קל להבין מהי תנועה הרמונית פשוטה באמצעות דוגמה של גוף שמחובר לקפיץ שבתורו מחובר לקיר. כדי שכוח המשיכה לא יתערב בעניין, נניח שהקפיץ והגוף מונחים על שולחן והקפיץ מתוח באופן אופקי. כעת, כל עוד הקפיץ ב”מנוחה”, לא קורה כלום; אבל אם נזיז את הגוף בכיוון המנוגד לקיר, הקפיץ יימתח; וכאשר נעזוב את הגוף, הקפיץ יתחיל למשוך את הגוף, כלומר להפעיל עליו כוח. הכוח הזה מתורגם לתאוצה של הגוף, כלומר לשינוי במהירותו; וזה מתורגם לשינוי במיקום הגוף; וזה מתורגם לשינוי באורך הקפיץ - הקפיץ מתחיל להתקצר, ולכן הכוח שהוא מפעיל על הגוף קטן. מתישהו הקפיץ יגיע לנקודת שיווי המשקל שלו ויפסיק לגמרי להפעיל כוח על הגוף, ולכן הגוף יפסיק להאיץ, אבל בינתיים הגוף כבר צבר מהירות כלשהי, ולכן הוא ימשיך בתנועתו ויתחיל לדחוס את הקפיץ, מה שיגרום לקפיץ להפעיל על הגוף כוח בכיוון המנוגד לכיוון תנועתו הנוכחי של הגוף. בסופו של דבר הגוף ייכנע ויתחיל לזוז לכיוון השני, גורר את הקפיץ איתו; ואז הקפיץ שוב יתארך, ויתחיל “למשוך” את הגוף חזרה לנקודת שיווי המשקל, וכן הלאה וכן הלאה. כל עוד כוחות חיצוניים לא מתערבים במשחק הזה, הוא יימשך בצורה מחזורית עד אין קץ. מחזורית, מה? הנה, כבר בתיאור הפיזיקלי המעורפל, צצים הסינוסים והקוסינוסים - הפונקציות המחזוריות ה”טבעיות” של המתמטיקה.

נעבור לתיאור המתמטי. אנחנו רוצים לתאר את מיקום הגוף כפונקציה של הזמן. בדרך כלל מסמנים את הפונקציה הזו בתור \( x\left(t\right) \) אבל זה כבר מבלבל מדי לטעמי, ולכן אקרא לה \( f\left(t\right) \) (שימו לב שכל התנועה היא חד ממדית, ולכן מספיק מספר בודד כדי לתאר את המיקום). המיקום מן הסתם צריך להימדד ביחס לאיזו ראשית צירים, וטבעי לבחור בנקודה שבה הקפיץ בשיווי משקל (כלומר, לא מפעיל כוח) בתור ראשית הצירים הזו. כעת, מבחינה פיזיקלית הכוח שקפיץ מפעיל על גוף הוא פרופורציוני למידת ההתארכות או הכיווץ של הקפיץ, ואצלנו מידת ההתארכות/כיווץ הזו היא בדיוק מיקום הגוף ביחס לראשית הצירים. דהיינו, הכוח שהקפיץ מפעיל על הגוף בזמן \( t \) הוא \( -k\cdot f\left(t\right) \), כאשר \( f\left(t\right) \) הוא כזכור מיקום הגוף באותו פרק זמן, ו-\( k \) הוא קבוע חיובי כלשהו התלוי רק בקפיץ. המינוס מתאר את העובדה שכאשר הקפיץ מתוח (ואז \( f\left(t\right)>0 \)) הקפיץ מושך את הגוף אליו, וכאשר הקפיץ דחוס (\( f\left(t\right)<0 \)) הקפיץ דוחה את הגוף ממנו והלאה.

כעת המהומה הדיפרנציאלית של המיקום-תלוי-בקצב-השינוי-של-המיקום-שתלוי-במיקום נכנסת לתמונה. לצורך פשטות המודל אני משתמש בגרסה הבסיסית ביותר של החוק השני של ניוטון: \( F=ma \), דהיינו התאוצה של הגוף היא פרופורציונית לכוח שמופעל עליו, כשקבוע הפרופורציה מכונה “מסה” והוא תמיד חיובי (אפשר לחשוב על המסה \( m \) בתור “כמות ההתנגדות להאצה” של הגוף). אבל מהי ה”תאוצה” הזו? כאמור, היא השינוי במהירות. ומהי המהירות? השינוי במיקום. כלומר, המהירות היא \( f^{\prime}\left(t\right) \) ואילו התאוצה היא \( f^{\prime\prime}\left(t\right) \). מכאן שקיבלנו את המשוואה הבאה: \( f^{\prime\prime}\left(t\right)=-\frac{k}{m}f\left(t\right) \). התקווה שלנו היא כי מהמשוואה הזו ניתן לחלץ את התיאור הסגור של \( f\left(t\right) \).

אם כן, הגענו למשוואה מסדר שני; משוואה שבה מופיעה הנגזרת השנייה של \( f \). עכשיו אפשר לרגע לשכוח מהמוטיבציה (אל חשש - בסוף אפתור גם את המשוואה הספציפית הזו!) ולעבור לדבר על משוואות מסדר שני באופן כללי. כרגיל, נתחיל מהפשוטה ביותר: \( f^{\prime\prime}=f \). כמו בסדר ראשון, \( f\left(x\right)=0 \) היא פתרון לא מעניין של המשוואה, ולכן אפשר לקבוע את תנאי ההתחלה הרגיל \( f\left(0\right)=1 \). “ניחוש” מוצלח מהיר יראה לנו ש-\( f\left(x\right)=e^{x} \) היא פתרון של המשוואה הזו - ולמה שלא תהיה? אם נגזרתה הראשונה שווה לעצמה, אותו הדבר יקרה גם בנגזת השנייה, ובכל נגזרת אפשרית. אם כן, האם לא קיבלנו שום דבר חדש?

התשובה שלילית. עוד קצת מחשבה יצירתית תראה לנו שיש למשוואה הזו, עם אותו תנאי התחלה, פתרון נוסף: \( e^{-x} \). זאת מכיוון ש-\( \left(e^{-x}\right)^{\prime}=-e^{-x} \), ולכן \( \left(e^{-x}\right)^{\prime\prime}=-\left(-e^{-x}\right)=e^{-x} \). אם כן, משפט הקיום והיחידות ששימש אותו במשוואות מסדר ראשון כבר לא תקף. מה שכן תקפה היא גרסה מתקדמת יותר שלו (וקשה יותר להוכחה) שאומרת שבתנאים כך וכך על המשוואה (שמתקיימים בכל המשוואות שעליהן אדבר), קיים למשוואה פתרון והוא יחיד אם נדרשים שני תנאי התחלה: \( f\left(x_{0}\right)=a_{0} \) ו-\( f^{\prime}\left(x_{0}\right)=b_{0} \), כלומר אנחנו אומרים מה יהיה ערכה של \( f \) ושל נגזרתה הראשונה של \( f \) בנקודה כלשהי. הפתרון \( e^{x} \) של המשוואה שלנו מתאים לתנאי ההתחלה \( f\left(0\right)=f^{\prime}\left(0\right)=1 \); והפתרון \( e^{-x} \) מתאים לתנאי ההתחלה \( f\left(0\right)=1,f^{\prime}\left(0\right)=-1 \).

שני הפתרונות שכבר מצאנו לא רק מעניינים לכשעצמם - הם גם מאפשרים לנו לפתור את המשוואה לכל זוג תנאי התחלה אחרים. הרעיון הוא פשוט - ראשית נשים לב לכך שאם \( f,g \) הן שני פתרונות של המשוואה (בלי תנאי התחלה), גם \( \alpha f+\beta g \) הוא פתרון, כאשר \( \alpha,\beta \) מספרים ממשיים כלשהם. הסיבה לכך היא שנגזרת היא לינארית, באופן שתואר כבר בפוסט הקודם: \( \left(\alpha f+\beta g\right)^{\prime}=\alpha f^{\prime}+\beta g^{\prime} \), ולא קשה להסיק מתכונה זו את הטענה שלי. מכאן שאם נדרשים מאיתנו שני תנאי התחלה ספציפיים, \( f\left(x_{0}\right)=a_{0} \) ו-\( f^{\prime}\left(x_{0}\right)=b_{0} \), אפשר לכתוב פתרון “כללי” למשוואה מהצורה \( \alpha f+\beta g \), להציב בו את \( x_{0} \) ולהציב ב-\( \alpha f^{\prime}+\beta g^{\prime} \)את \( x_{0} \), ואז לקבל שתי משוואות בשני נעלמים - הנעלמים \( \alpha,\beta \). עם “קצת מזל” יהיה למשוואה זו פתרון. התיאוריה המדוייקת עוסקת מן הסתם בפורמליזציה של ה”קצת מזל” הזה (מילת הקסם “ורונסקיאן” נכנסת לתמונה) אבל כאמור, כרגע איני מנסה לכתוב ספר מד”ר ולא אכנס לכך. במקום זה אסתפק בבדיקת מקרה פרטי אחד או שניים.

בואו נגיד, למשל, שאנחנו רוצים בתור תנאי התחלה למשוואה שיתקיים \( f\left(0\right)=1 \) אבל \( f^{\prime}\left(0\right)=0 \). האם זה אפשרי בכלל? בואו ננסה: נכתוב “פתרון כללי” \( ae^{x}+be^{-x} \), נציב בו \( 0 \) ונקבל את המשוואה \( a+b=1 \). נגזור את הפתרון הכללי ונקבל \( ae^{x}-be^{-x} \), נציב בזה \( 0 \) ונקבל את המשוואה \( a-b=0 \), שממנה נגזר \( a=b \). נציב זאת במשוואה הראשונה ונקבל \( a=b=\frac{1}{2} \), כלומר הפתרון שרצינו, שמקיים את תנאי ההתחלה שלנו, הוא \( \frac{e^{x}+e^{-x}}{2} \) (בהערת אגב, הפונקציה הזו היא בעלת חשיבות רבה בפני עצמה עד שזכתה לשם “קוסינוס היפרבולי”; ועל כך - בפוסט אחר, ביום מן הימים). בתור תרגיל אפשר לנסות ולעשות את אותו תעלול עבור תנאי ההתחלה \( f\left(0\right)=f^{\prime}\left(0\right)=0 \) ולראות שמקבלים את הפתרון \( a=b=0 \), כלומר הפונקציה \( f\left(x\right)=0 \) צצה מאליה במסגרת הטיפול הכולל במשוואה ולא צריך להתעסק איתה באופן פרטני.

אותה שיטה תקפה באופן כללי למשוואות מסדר שני שבהן אין גורם “חופשי” (שבו לא מופיעה \( f \) או נגזרת שלה) - מוצאים שני פתרונות “בלתי תלויים” ואז כל הפתרונות נתונים כצירוף לינארי של שני הפתרונות שנמצאו. חמושים בידע הזה הבה ונתקוף את המשוואה הכללית ביותר שבה אין גורם חופשי וכל המקדמים הם קבועים - משוואה מהצורה \( af^{\prime\prime}+bf^{\prime}+cf=0 \). האינסטינקט הראשון הוא להציב במשוואה הזו שוב וריאציה על \( e^{x} \), שהיה הקלף המנצח שלנו עד כה - הבה ונציב בה את \( e^{\lambda x} \) עבור \( \lambda \) ממשי כלשהו. מכיוון ש-\( \left(e^{\lambda x}\right)^{\prime}=\lambda e^{\lambda x} \), ו-\( \left(e^{\lambda x}\right)^{\prime\prime}=\lambda^{2}e^{\lambda x} \), הרי שאחרי ההצבה נקבל כי \( a\lambda^{2}e^{\lambda x}+b\lambda e^{\lambda x}+ce^{\lambda x}=0 \), ואחרי הוצאת גורם משותף, \( \left(a\lambda^{2}+b\lambda+c\right)e^{\lambda x}=0 \). כעת ניזכר כי פונקצית האקספוננט אינה מתאפסת בשום נקודה (אחרת הייתה אפס בכל מקום) ולכן אפשר לצמצם בה, ולהיוותר עם \( a\lambda^{2}+b\lambda+c=0 \). במילים אחרות, אם \( e^{\lambda x} \) הוא פתרון למשוואה הדיפרנציאלית, אז \( \lambda \) הוא פתרון למשוואה הריבועית \( ax^{2}+bx+c \). שלום כיתה א’.

כזכור מכיתה א’ (יותר נכון, מחטיבת הביניים) למשוואה ריבועית יכולים להיות שני פתרונות, פתרון אחד, או “אפס” פתרונות, בהתאם לשאלה האם הפרבולה שמוגדרת באמצעות \( y=ax^{2}+bx+c \) חותכת את ציר ה-\( x \) (2 פתרונות), משיקה לו (פתרון יחיד) או מרחפת מעליו או מתחתיו (“אפס” פתרונות). במקרה שבו ישנם שני פתרונות, \( \lambda_{1},\lambda_{2} \) קיבלנו שני פתרונות למשוואה הדיפרנציאלית: \( e^{\lambda_{1}x},e^{\lambda_{2}x} \). חישוב לא מסובך בעזרת אותו ורונסקיאן פלאי מראה שמכיוון ש-\( \lambda_{1}\ne\lambda_{2} \) הרי ש”יש לנו מזל” ושני הפתרונות הללו פורשים את מרחב הפתרונות כולו, וזה סוף הסיפור. עבור המשוואה \( f^{\prime\prime}=f \) זה עובד יופי: אפשר לכתוב אותה גם כ-\( f^{\prime\prime}-f=0 \), כלומר \( a=1,b=0,c=1 \) וקיבלנו את המשוואה \( \lambda^{2}-1=0 \) שפתרונותיה הם \( \lambda=\pm1 \), ואכן הפתרונות הפורשים שמצאנו היו \( e^{x},e^{-x} \).

אם לעומת זאת למשוואה היה פתרון יחיד (למשל, למשוואה \( x^{2}-2x+1=0 \) קיים רק הפתרון \( 1 \), שכן דרך אחרת לכתוב את המשוואה הזו היא בתור \( \left(x-1\right)^{2}=0 \)) הרי ש”אכלנו אותה” - כל השיטה המפוארת שלנו ל”ניחוש” פתרון הניבה רק חצי מכמות הפתרונות שצריכים, ואנחנו צריכים למצוא פתרון נוסף, בלתי תלוי בראשון, באמצעות קסמים חדשים. יש קסמים כאלו, אבל כרגיל - אני לא כותב ספר מד”ר ולא אכנס לכך כעת. המקרה שבאמת מעניין אותי בכל הסיפור הזה הוא המקרה השלישי, זה שבו יש “אפס” פתרונות. כמו שאפשר לנחש מהמרכאות שאני כל הזמן כותב, ממש לא נכון לומר (כמו שלמדנו בחטיבת הביניים) שלמשוואה יש אפס פתרונות; כל מה שאפשר לומר הוא שיש לה אפס פתרונות ממשיים, אבל למה להגביל את עצמנו? כאשר מתירים פתרונות מרוכבים (כלומר, כאשר מסתכלים על שדה ההרחבה הטבעי של הממשיים - אנחנו לא מוסיפים כאן פתרונות מלאכותיים) רואים שלמשוואה יש במקרה זה שני פתרונות מרוכבים. מכיוון שהמשוואה היא בעלת מקדמים ממשיים, אז אם \( z \) המרוכב הוא פתרון של המשוואה, כך גם \( \overline{z} \), הצמוד המרוכב שלו (ההוכחה לכך פשוטה: אם \( az^{2}+bz+c=0 \), הרי שאחרי ש”נצמיד” את כל המשוואה ונשתמש בכך שצמוד של מספר ממשי הוא אותו מספר עצמו, נקבל \( 0=\overline{0}=\overline{az^{2}+bz+c}=\overline{a}\overline{z}^{2}+\overline{b}\overline{z}+\overline{c}=a\overline{z}^{2}+b\overline{z}+c \)), ומכאן שהפתולוגיה של “יש רק פתרון אחד! מה נעשה, מה נעשה” לא מתרחשת במקרה הזה, ושני הפתרונות שקיבלנו הם תמיד בעלי קשר הדוק זה לזה: \( e^{\lambda x} \) ו-\( e^{\overline{\lambda}x} \), ומכאן ש…

רגע, רגע, רגע. לא כל כך מהר. בספרי המד”ר בשלב זה מקדישים דיון קצר לשאלה מהו אקספוננט שמועלה בחזקת מספר מרוכב ומגיעים מיידית לנוסחת אוילר. אלא שנוסחת אוילר מניחה שכבר קיימים סינוסים וקוסינוסים, ואילו המטרה שלי כרגע היא לתת מוטיבציה להגדרת הפונקציות הללו ולדיון עליהן, ולכן אני מגיע כעת לפרשת דרכים: האם אני רוצה לתאר את נוסחת אוילר, שאומרת ש-\( e^{i\theta}=f\left(\theta\right)+ig\left(\theta\right) \) עבור שתי פונקציות ממשיות מאוד מסויימות \( f,g \), ואז לקרוא להן \( \cos \) ו-\( \sin \) בהתאמה? יש הגיון בגישה הזו, שבשורה התחתונה אומרת שקוסינוס וסינוס הן פונקציות ההיטל של פונקצית האקספוננט המרוכב (שהוא בתורו הרחבה טבעית של האקספוננט הממשי, שאותו תיארתי בפוסט הקודם). עם זאת, אני רוצה לאמץ גישה שונה, אולי מעט יותר מוגבלת ברוחב המבט שלה שכן היא לא תתבונן על המרוכבים, אבל יותר דומה באופיה ה”חקרני” לנקודת המבט שאימצתי בפוסט על האקספוננט, ולנסות להמציא את סינוס וקוסינוס בנפרד מהאקספוננט, ורק בסוף לקשור בין כולם.

אם כן, הפוסט הבא יעסוק בחיפוש אחר הפתרונות למשוואה הפשוטה ביותר ש”עושה בעיות” - המשוואה \( f^{\prime\prime}=-f \). יהיה אקשן.