אז מה זו בעצם חבורה?

את סדרת הפוסטים שלי על אלגברה מופשטת אני רוצה להתחיל עם המושג שבדרך כלל מתחילים ממנו ספרים באלגברה מופשטת - חבורה. זה לא המושג הראשון שסטודנטים נתקלים בו (לרוב הם פוגשים קודם שדות ומרחבים וקטוריים) וגם לא המושג הפשוט ביותר, אבל הוא פשוט דיו ושימושי דיו כדי להוות נקודת התחלה טובה. אז בואו ננסה להבין מהו. חבורה היא מושג מופשט - אנחנו מזהים כמה תכונות מעניינות בהרבה אובייקטים מתמטיים קונקרטיים שמעניינים אותנו ושואלים את עצמנו מה אפשר להסיק מתוך התכונות הללו לבד, בלי שאר האינפורמציה שיש לנו על האובייקטים הקונקרטיים הללו. אז בואו נתחיל מלהיזכר בכמה אובייקטים קונקרטיים שכאלו.

הדוגמה הראשונה, וכזו שיש לה חשיבות מרכזית בנושא הזה, היא המספרים השלמים - \( \mathbb{Z}=\left\{ 0,1,-1,2,-2,\dots\right\} \) שאני מניח שאתם כבר מכירים. על המספרים השלמים מוגדרות כמה פעולות חשבון; בואו נתחיל עם פעולת החיבור. חיבור הוא פעולה בינארית - אנחנו תמיד מחברים ביחד רק שני מספרים, והתוצאה היא מספר שלם חדש. למשל \( 5+2=7 \). אבל מה קורה אם אנחנו רוצים לחבר שלושה מספרים שלמים? אנחנו רגילים לכתוב משהו כמו \( 5+2+3=10 \) בלי לחשוב על זה, אבל קורה כאן משהו מאחורי הקלעים - אנחנו קודם כל מבצעים פעולת חיבור אחת, נאמר של \( 5+2 \), ואז את התוצאה שקיבלנו אנחנו מחברים עם המספר שנותר. במילים אחרות, אנחנו לא מבצעים חיבור של שלושה מספרים בו זמנית אלא קודם מחברים שני מספרים, מקבלים תוצאת ביניים, ואת תוצאת הביניים הזו מחברים עם המספר השלישי. וכאן בא לידי ביטוי כלל שאנחנו מכירים מבית הספר היסודי ונקרא כלל הקיבוץ שאומר שאם אנחנו מחברים שלושה מספרים בצורה כזו, זה לא משנה את איזו מפעולות החיבור נבצע קודם, בכל מקרה נקבל את אותה התוצאה. כלומר, \( \left(5+2\right)+3=5+\left(2+3\right) \) (באגף שמאל תוצאת הביניים היא 7 ואותה מחברים ל-3; באגף ימין תוצאת הביניים היא 5 ואותה מחברים ל-5). ברשותכם, מעתה והלאה במקום לומר “חוק הקיבוץ” אשתמש במושג הלועזי, אסוציאטיביות.

אנחנו כל כך רגילים לאסוציאטיביות שכדאי תכף ומייד לראות פעולה שלא מקיימת אסוציאטיביות, כדי שנבין שהתכונה הזו אינה מובנת מאליה. הפעולה שאינה אסוציאטיבית היא חיסור: מצד אחד, \( \left(5-2\right)-3=0 \); מצד שני, \( 5-\left(2-3\right)=6 \), ולכן בוודאי שלא מתקיים \( \left(5-2\right)-3=5-\left(2-3\right) \). למרות זאת אנחנו כותבים ביטויים כמו \( 5-2-3 \) שהם נטולי סוגריים, כי יש לנו מוסכמה שכבר התרגלנו אליה לפיה כשיש חשיבות לסדר שבו מבצעים שתי פעולות, הסדר הוא “משמאל לימין”, דהיינו קודם מבצעים את הפעולה השמאלית יותר. כלומר הביטוי \( 5-2-3 \) הוא כתיב נטול סוגריים לביטוי \( \left(5-2\right)-3 \).

עוד דבר שאנחנו יודעים שמתקיים במספרים השלמים הוא שיש למספר אפס תכונה מיוחדת - אם מחברים אותו למספר כלשהו, המספר לא משתנה. \( 5+0=5 \). התכונה הזו גרמה למהומות פילוסופיות לא קטנות בשעתו (אם אפס הוא “מספר” שבכלל לא משנה את מי שהוא מתחבר אליו, האם נכון לקרוא לו “מספר”?) אבל אנחנו כבר רגילים אליה הן מבית הספר והן מחיי היום יום. עוד דבר שעורר בשעתו מהומות אדירות ואנחנו רגילים אליו הוא קיום מספרים שליליים. אבל מהו מספר שלילי? ובכן, “מינוס 5” הוא המספר שכאשר מחברים אותו אל 5, מקבלים 0. בניסוח פורמלי, \( 5+\left(-5\right)=0 \). אם נחשוב על זה רגע, נראה שבמספרים השלמים המשמעות של “חיסור” היא בסך הכל “חיבור עם המינוס”. במקום לחסר 5, אפשר לחבר מינוס 5. המינוס של מספר מכונה גם ה”נגדי” שלו.

אם כן, ציינתי כאן שלוש תכונות של השלמים: החיבור שלהם אסוציאטיבי, קיים איבר אדיש ביחס לחיבור, ולכל איבר קיים איבר נגדי ביחס לחיבור. אלו שלוש התכונות שיעניינו אותנו ונשתמש בהן כדי להגדיר חבורה. שימו לב איך אנחנו משמיטים החוצה כל מני דברים אחרים על המספרים השלמים שאתם כנראה גם כן מכירים. למשל, את חוק החילוף שאומר ש-\( a+b=b+a \) לא הכנסתי לתמונה (אבל הוא יצטרף עוד מעט). את פעולת הכפל ואת חוק הפילוג שמתקשר אליה גם כן לא הכנסתי לתמונה, וכן הלאה. זה הרעיון בהפשטה - לא חייבים לקחת הכל. לוקחים חלק שהוא מספיק כדי לקבל משהו מעניין ושימושי בפני עצמו.

בואו נראה עוד דברים שמקיימים את שלוש התכונות הללו. אני צריך לציין קבוצה של איברים עם פעולה עליה. ראשית כל, מספרים! למה להסתפק בשלמים כשיש גם את המספרים הרציונליים \( \mathbb{Q} \) ואת המספרים הממשיים \( \mathbb{R} \) ואת המספרים המרוכבים \( \mathbb{C} \)? גם כל המספרים הללו מהווים חבורה ביחס לפעולת החיבור. ומה עם המספרים הטבעיים, \( \mathbb{N} \)? הם לא חבורה מכיוון שאין לנו איברים נגדיים: למשל, אין מספר טבעי שאפשר לחבר ל-1 כדי לקבל את 0. למעשה, השאלה היא 0 בעצמו הוא מספר טבעי היא כזו שאין עליה קונצנזוס; כל ספר עשוי להגדיר אחרת. לכן ייתכן שהטבעיים ייכשלו בנסיון להיות חבורה כבר עם הדרישה לקיום איבר אדיש.

עד עכשיו דיברנו על מספרים עם פעולת החיבור. אבל מה עם פעולת הכפל? זו בוודאי פעולה אסוציאטיבית, ויש לנו איבר אדיש ביחס אליה: \( 1 \). אבל החלק עם הנגדי עושה לנו בעיות. בואו נדבר לרגע על המספרים השלמים - האם קיים מספר שלם \( x \) כך ש-\( 2\cdot x=1 \)? התשובה שלילית. אז השלמים לא מהווים חבורה ביחס לכפל. אבל מה עם הרציונליים, שבהם למשוואה \( 2\cdot x=1 \) יש פתרון? הם כמעט עובדים, אבל יש לנו בעיה נקודתית אחת: המספר המעצבן \( 0 \). אפשר להראות ש-\( x\cdot0=0 \) לכל \( x \) ולכן למשוואה \( x\cdot0=1 \) אין פתרון - כלומר, לאפס לא יהיה איבר נגדי ביחס לכפל. עם זאת, אם מעיפים החוצה את 0, כן נקבל חבורה. אני מסמן ב-\( \mathbb{Q}^{*} \) את קבוצת הרציונליים למעט 0; זוהי חבורה ביחס לפעולת הכפל. בדומה אפשר לדבר גם על \( \mathbb{R}^{*} \) ו-\( \mathbb{C}^{*} \) שכולן חבורות ביחס לפעולת הכפל.

אבל מה עם דברים שהם לא מספרים? אם אתם מכירים אלגברה לינארית, אתם בוודאי מכירים מטריצות. על מטריצות מוגדרת פעולת כפל מטריצות שהיא משהו בעל אופי די שונה מכפל רגיל של מספרים (למשל, היא לא מקיימת את חוק החילוף) אבל היא עדיין מקיימת את תכונת האסוציאטיביות (להוכיח את זה, זו עבודה טכנית לא נעימה). האם כל קבוצה של מטריצות תהיה חבורה? לא; אנחנו צריכים לדרוש במפורש ראשית שהמטריצות יהיו ריבועיות (אחרת לא יהיה ניתן לכפול כל זוג מטריצות מהקבוצה), ושכל המטריצות שאנחנו כופלים תהיינה הפיכות, אחרת לא יהיה קיים איבר “נגדי” ביחס לפעולת כפל המטריצות. ונצטרך גם לוודא שמטריצת היחידה (המטריצה שכולה אפסים למעט האלכסון הראשי שכולו 1-ים) תהיה בפנים. יש כל מני קבוצות מעניינות של מטריצות שמקיימות את זה, והדוגמה הראשונה שקופצת לראש היא הקבוצה שמסומנת בתור \( \text{GL}_{n}\left(\mathbb{R}\right) \) - קבוצת כל המטריצות ההפיכות מסדר \( n\times n \) מעל השדה \( \mathbb{R} \). הקבוצה הזו תהיה חבורה ביחס לפעולת כפל מטריצות.

הנה עוד דוגמה חשובה: נניח ש-\( A \) היא קבוצה כלשהי. אז אפשר לדבר על פונקציות \( f:A\to A \) מהקבוצה לעצמה. כזכור, פונקציה היא חד-חד-ערכית אם \( f\left(x\right)=f\left(y\right) \) גורר ש-\( x=y \) (אין שני קלטים שונים שנותנים את אותו הפלט) והיא על אם לכל \( y\in A \) קיים \( x\in A \) כך ש-\( f\left(x\right)=y \) (כל פלט מתקבל מהפעלת \( f \) על קלט כלשהו). לא קשה להראות שפונקציה היא בו זמנית חד-חד-ערכית וגם על אם ורק אם היא הפיכה (קיימת \( f^{-1} \) כך שמתקיימת התכונה \( f^{-1}\left(f\left(x\right)\right)=x \) וגם \( f\left(f^{-1}\left(x\right)\right)=x \) לכל \( x\in A \)). מכאן קצרה הדרך לכך שנראה שקבוצת כל הפונקציות מ-\( A \) לעצמה שהן חד-חד-ערכיות ועל היא חבורה (האיבר האדיש הוא הפונקציה \( f\left(x\right)=x \)). בהקשר של תורת החבורות נהוג לכנות פונקציות כאלו בשם תמורות; אנחנו הולכים לדבר הרבה על תמורות בהמשך, בעיקר במקרה שבו \( A \) היא קבוצה סופית; המחקר של חבורות של תמורות היה הכוח המניע המרכזי בראשית ימי תורת החבורות, עוד לפני שהתחילו לדבר על המושג המופשט של חבורה.

והנה עוד דוגמה שהייתה כוח מניע: המספרים השלמים מודולו \( n \). אנחנו נראה את הדוגמה הזו בפירוט וגם יש לי כבר פוסט בבלוג על חשבון מודולרי, אז כאן אזכיר אותה מאוד בקצרה: חשבון מודולו \( n \) על מספרים שלמים פירושו לבצע את פעולת החשבון הרגילה, אבל אז לחלק את התוצאה ב-\( n \) ולקחת את השארית. למשל, \( 5+8 \) מודולו 4 יוצא 1, כי \( 5+8=13 \) ואחרי חלוקה ב-4 נקבל שארית 1. ב-\( \mathbb{Z}_{n} \) מסמנים את קבוצת המספרים השלמים מ-0 עד \( n-1 \), עם פעולת החיבור מודולו \( n \); אפשר להראות שזוהי חבורה. ב-\( \mathbb{Z}_{n}^{*} \) מסמנים את קבוצת השלמים עם פעולת כפל מודולו \( n \), כאשר השלמים ששייכים לקבוצה הם המספרים מ-\( 0 \) עד \( n-1 \) שקיים להם הופכי מודולו \( n \); אפשר להוכיח שאלו בדיוק המספרים שזרים ל-\( n \) (שהמחלק המשותף הגדול ביותר שלהם ושל \( n \) הוא 1). למשל, \( \mathbb{Z}_{8}^{*} \) היא קבוצת המספרים \( \left\{ 1,3,5,7\right\} \). אם נכפול, למשל, את \( 3 \) ב-5 וניקח את התוצאה מודולו 8 נקבל 7, ובאופן כללי אם ניקח זוג מספרים מהקבוצה ונכפול אותם נקבל מספר אחר מהקבוצה.

ראינו כמה דוגמאות מרכזיות, אם כי זה בוודאי עוד לא סוף הסיפור, ואני חושב שזה זמן טוב לכתוב במפורש את ההגדרה הפורמלית של חבורה. אם כן, חבורה היא זוג \( \left(G,\cdot\right) \) של קבוצה \( G \) ופעולה בינארית על \( G \) שלרוב מסומנת בעזרת סימן הכפל (כלומר, כותבים \( a\cdot b \) או אפילו זה לא ופשוט כותבים \( ab \) כדי לתאר את הכפל של \( a \) ב-\( b \)). כשאני אומר “פעולה בינארית” אני מתכוון, פורמלית, לפונקציה מ-\( G\times G \) אל \( G \). כלומר, עוד לפני שהגענו לתכונות שאנחנו דורשים מהפעולה הזו לקיים כבר הנחנו משהו שנקרא סגירות - התוצאה של הפעלת הפעולה הבינארית לא מוציאה אותנו מהקבוצה. עכשיו אנחנו דורשים את שלוש התכונות הבאות:

• לכל \( a,b,c\in G \) מתקיים \( \left(ab\right)c=a\left(bc\right) \) (אסוציאטיביות)
• קיים \( e\in G \) כך שלכל \( a\in G \) מתקיים \( ae=ea=a \) (איבר אדיש)
• לכל \( a\in G \) קיים \( a^{-1}\in G \) כך ש=\( aa^{-1}=a^{-1}a=e \) (איבר הופכי)

שלוש הדרישות הללו נקראות לפעמים האקסיומות של תורת החבורות. כאן המשמעות של “אקסיומה” היא כמובן לא “משהו שנכונותו מובנית מאליו” אלא “הנחת יסוד שעל הבסיס שלה אנחנו מוכיחים דברים”.

יש משהו שכדאי להבהיר עם הקטע הזה של איבר הופכי. ראשית, שימו לב שהתחלתי להגיד “הופכי” במקום “נגדי”, כי אני מסמן את הפעולה של החבורה בתור “כפל” ובכפל רגיל אם \( a\cdot x=1 \) אומרים ש-\( x \) הוא ההופכי של \( a \), לא הנגדי שלו. שנית, אני משתמש בסימון \( a^{-1} \) כדי לתאר את ההופכי של \( a \), אבל זה סימון בלבד - אני לא באמת מעלה פה שום דבר בחזקה, עוד לא הגדרתי מה זו חזקה של איבר בחבורה בכלל. אני רק אומר: קחו את \( a \). אז אני מבטיח לכם שקיים איבר כלשהו - ובואו נסמן אותו ב-\( a^{-1} \) - שכאשר כופלים אותו ב-\( a \) מקבלים את \( e \).

כעת, חוק החילוף לא מופיע כאן, אבל בהרבה חבורות הוא כן מתקיים - למשל, במספרים השלמים/רציונליים/ממשיים/מרוכבים עם פעולות החיבור והכפל כן מתקיים חוק החילוף, בזמן שעם תמורות או מטריצות הוא לא מתקיים. לכן אנחנו רוצים לתת שם מיוחד לחבורות שבהן הפעולה מקיימת את חוק החילוף:

• אם לכל \( a,b\in G \) מתקיים \( ab=ba \) אומרים שהחבורה היא אבלית.

המילה “אבלית” כאן היא על שם המתמטיקאי הנרווגי אבל (Niels Henrik Abel). השם הלועזי של חוק החילוף הוא קומוטטיביות, וגם במילה הזו אשתמש פה ושם. כבר בשלב הזה אגיד שחבורות אבליות וחבורות לא אבליות הם עולמות שונים ומשונים - את החבורות האבליות אנחנו מבינים “לא רע” בזמן שחבורות לא אבליות הן כאוס וטירוף ומהומות.

בשלב הזה ייתכן שאנחנו תוהים מה בכלל אפשר לעשות אם כל מה שיש לנו הוא שלוש האקסיומות הטריוויאליות הללו. אז בואו נראה תוצאה לא כל כך טריוויאלית ועם שלל השלכות שאפשר להוכיח מייד. נניח שיש לנו חבורה \( G \) (מכאן ואילך כשאני כותב \( G \) תמיד ההנחה תהיה שזו איזו חבורה) וניקח \( a\in G \) כלשהו. עכשיו, נניח שמתקיים \( ax=ay \) עבור שני איברים \( x,y\in G \). אני טוען ש-\( x=y \), כלומר שהפעולה “לכפול ב-\( a \) משמאל” היא חד-חד-ערכית. איך מוכיחים את זה? כופלים את שני האגפים משמאל ב-\( a^{-1} \) ומקבלים \( a^{-1}\left(ax\right)=a^{-1}\left(ay\right) \). עכשיו משתמשים באסוציאטיביות: \( \left(a^{-1}a\right)x=\left(a^{-1}a\right)y \). עכשיו משתמשים בתכונות של האיבר ההופכי: \( ex=ey \). עכשיו משתמשים בתכונות של האדיש: \( x=y \).

קשה להפריז בחשיבות של התכונה הזו. היא אומרת שאם אנחנו לוקחים איבר \( a \) וכופלים בו את כל אברי \( G \), נקבל שוב בדיוק את אברי \( G \), כל אחד בדיוק פעם אחת. כלומר, הפונקציה של “להכפיל ב-\( a \)” היא תמורה על \( G \) עצמה. יש לזה שלל שימושים, ונראה עכשיו רק אחד או שניים פשוטים. ראשית, אני רוצה להוכיח שהאיבר האדיש בחבורה הוא יחיד. כלומר, שאם יש לי שני איברים \( e_{1},e_{2} \) ששניהם מקיימים את התכונה \( e_{1}x=xe_{1}=x \) ו-\( e_{2}x=xe_{2}=x \) אז \( e_{1}=e_{2} \). זה נכון בגלל ש-\( ae_{1}=a=ae_{2} \) (וזה גם נכון כי \( e_{1}=e_{1}e_{2}=e_{2} \) אבל נעזוב את זה). באופן דומה גם ההופכי הוא יחיד: בהינתן \( a \), אם \( ax=e=ay \) אז \( x=y \), ולכן יש רק איבר אחד שמקיים \( ax=e \). זה מצדיק את הדיבור על ההופכי של \( a \) (בה’ הידיעה).

בואו ננצל את מה שראינו עד כה כדי להתחיל להתמודד עם השאלה הראשונה שעולה מעצמה (נניח…) כשמתחילים לדבר על חבורות - אילו חבורות קיימות? יש המון כאלו, מן הסתם, אז אפשר להתחיל לסווג מהקל לקשה: קודם כל נבדוק מה החבורות עם איבר אחד; אחר כך מה החבורות עם שני איברים, וכן הלאה, ונראה האם בשלב כלשהו זה נהיה משוגע מדי בשבילנו.

חבורה עם איבר אחד זה קל: האיבר הזה חייב להיות \( e \) ולכן זו פשוט הקבוצה \( \left\{ e\right\} \) עם הפעולה \( e\cdot e=e \). ומה עם חבורות עם שני איברים? נקרא לאיברים \( \left\{ e,a\right\} \). אנחנו יודעים שבהכרח \( e\cdot e=e \) ו-\( e\cdot a=a\cdot e=a \), ולכן רק נשאר לברר מה חייב להיות \( a\cdot a \). ממה שראינו קודם, הכפלה ב-\( a \) היא תמורה, ולכן אם \( a\cdot e \) החזיר \( a \), אז ל-\( a\cdot a \) אין ברירה - הוא חייב להחזיר את האיבר האפשרי האחר, כלומר \( a\cdot a=e \). בגלל ה”אין ברירה” הזה אנחנו רואים שיש רק חבורה אחת עם שני איברים, עד כדי השמות שאנחנו נותנים לאיברים (אני אבהיר את העניין הזה בהמשך, כשנדבר על הומומורפיזמים). האם אנחנו מכירים סימון נחמד לחבורה הזו? כן! זה מה שקראנו לו קודם \( \mathbb{Z}_{2} \) והגדרנו בתור הקבוצה \( \left\{ 0,1\right\} \) עם חיבור מודולו 2. למרות שזו חבורה כמעט בנאלית, היא מאוד חשובה ושימושית בשלל הקשרים. כמובן, אפשר גם לקרוא לחבורה עם האיבר היחיד שראינו בשם \( \mathbb{Z}_{1} \) אם זה עושה לנו טוב.

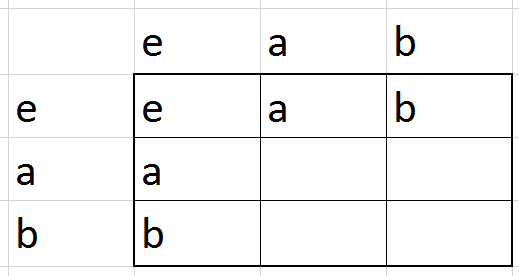
מה שאנחנו רואים מהדוגמה האחרונה הוא שניתוח של חבורות יכול מהר מאוד להפוך למסורבל. הרבה מאוד תלוי באופן שבו אנחנו מייצגים את החבורה. אני צריך איכשהו לתת אינפורמציה שתאפשר לנו לדעת באופן חד ערכי גם מיהם אברי \( G \) (אבל זה קל, פשוט נותנים להם שמות או ממספרים אותם או משהו) וגם מהי הפעולה הבינארית שמוגדרת על \( G \) - כלומר, אני צריך דרך כלשהי לדעת לכל זוג איברים מה קורה כשכופלים אותם. ייצוג בסיסי של דבר כזה הוא פשוט באמצעות טבלה דו-ממדית: “לוח כפל”. למשל, את החבורה עם שני איברים שלי יכלתי לכתוב כך:

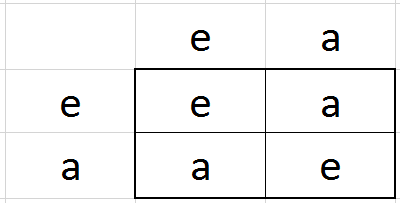
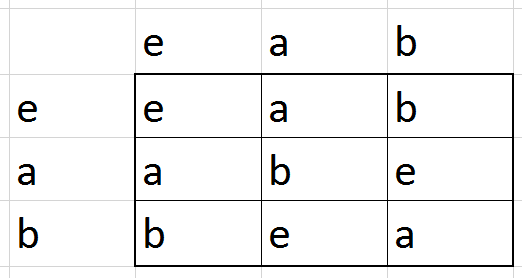
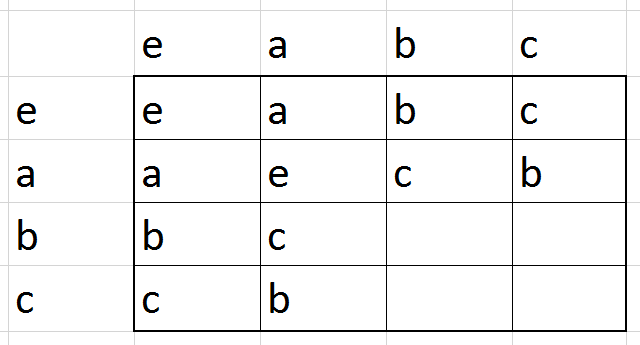
הרעיון פה הוא שבכל שורה אנחנו מציגים את תוצאת הכפל של האיבר שמתאים לאותה שורה בכל האיברים שמתאימים לעמודות (האיבר של השורה משמאל, האיברים של העמודות מימין). הכלל של “כפל באיבר הוא תמורה” אומר לנו שבכל שורה צריכים להופיע כל אברי החבורה - ובדומה, כך גם בכל עמודה. במילים אחרות, יש לנו כאן סוג של משחק סודוקו: אין לנו חופש למלא את טבלת הכפל של חבורה איך שבא לנו, אנחנו צריכים לציית לכללים בסיסיים שמגבילים אותנו. בואו ננסה לעשות את זה עם חבורה בת 3 איברים שנסמן \( e,a,b \):

עד כה מילאתי בטבלה רק את השורה והעמודה הראשונים, של \( e \); כאן אין לי בחירה בכלל בגלל האופן שבו \( e \) מתנהג. הבחירה הראשונה שלי היא מה לעשות עבור הכניסה של המכפלה \( a\cdot a \). האם אני יכול לבחור שהכניסה הזו תהיה \( a \)? לא! כי הכניסה הקודמת, משמאל לכניסה הזו, כבר הייתה \( a \) ואסור שני \( a \) באותה שורה. והאם אני יכול להגדיר \( a\cdot a=e \)? על פניו כן, אבל שימו לב למה זה יוביל: האיבר האחרון בשורה יהיה חייב להיות \( b \), וזה יתנגש עם זה שבעמודה שלו כבר יש \( b \). סודוקו, כאמור. לכן אני חייב לבחור \( a\cdot a=b \) ואז נקבל את הטבלה:

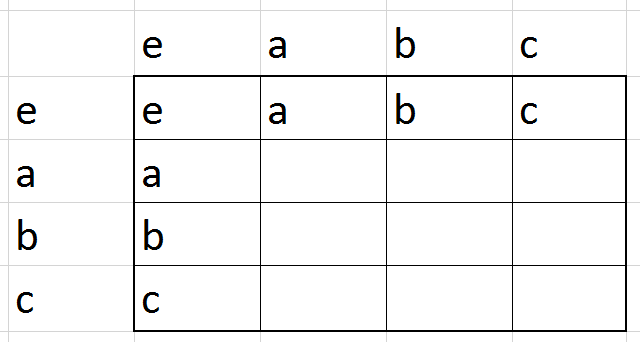
גם פה הטבלה נקבעה באופן יחיד - יש רק חבורה אחת עם \( 3 \) איברים, והיא, שלא במפתיע, \( \mathbb{Z}_{3} \) (ובאמת, \( 1+1=2 \) ו-\( 2+2=1 \) כאשר החיבור הוא מודולו 3). בשלב הזה אנחנו מתחילים לחשוד שלכל מספר טבעי קיימת רק חבורה אחת מאותו הגודל, והאקשן האמיתי הוא רק בחבורות אינסופיות (רוב הדוגמאות שלי…). אבל בואו נראה מה קורה עם ארבעה איברים, \( e,a,b,c \):

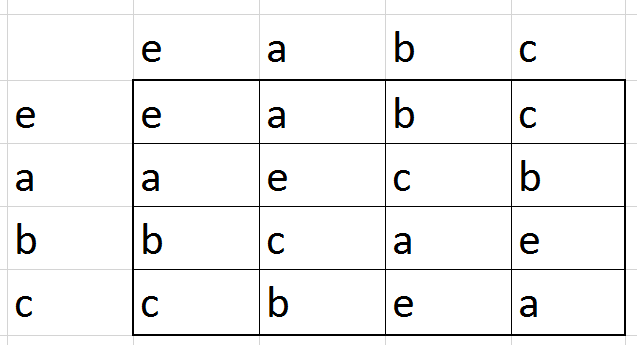
כאן יש לנו חופש בחירה גדול יחסית של מה יהיה \( a\cdot a \) - פרט לכך שאנחנו לא יכולים לבחור \( a\cdot a=a \), כל אפשרות אחרת עובדת. אם נבחר \( a\cdot a=e \), המשך השורה ייקבע בצורה שמטרתה למנוע התנגשות עם העמודה שמעל, ולכן נקבל:

עכשיו יש לנו חופש בחירה גם עבור \( b\cdot b \) שיכול להיות \( e \) או \( a \). בואו נתחיל מ-\( b\cdot b=a \). נקבל:

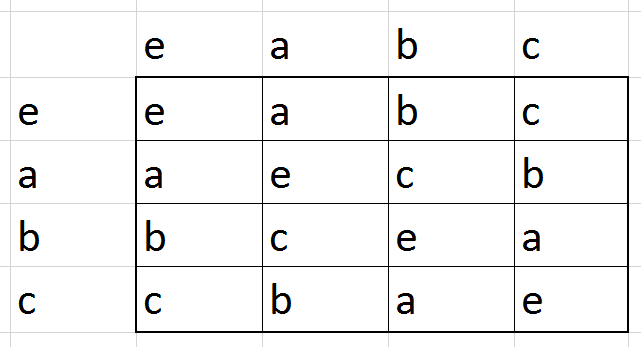
מה קיבלנו כאן? את החבורה \( \mathbb{Z}_{4} \) בתחפושת. כאן \( a=2 \) ואילו \( b,c \) הם \( 1,3 \) (לא משנה מי הוא מי). בחירות אחרות בשלבים מוקדמים יותר יובילו אותנו גם כן לוריאציות על החבורה הזו. אבל כן יצוץ גם דבר אחד חדש: אם בשלב הקודם היינו בוחרים \( b\cdot b=e \) היינו מקבלים את טבלת הכפל

וכאן מתקיים משהו חדש: חבורה בת ארבעה איברים שבה המכפלה של כל איבר עם עצמו היא \( e \), והמכפלה של כל זוג איברים שונים מ-\( e \) נותנת את האיבר השלישי. זו לא \( \mathbb{Z}_{4} \) אלא חבורה חדשה, מסוג שלא ראינו קודם. בואו נראה עוד דרך לתאר אותה: אני אסמן אותה בסימון \( \mathbb{Z}_{2}\times\mathbb{Z}_{2} \) ואגדיר אותה כאוסף הזוגות \( \left(a,b\right) \) שבהם \( a,b \) הם 0 או 1, וחיבור הוא מודולו 2 ו-“רכיב-רכיב”, כלומר \( \left(a,b\right)+\left(x,y\right)=\left(a+x,b+y\right) \). לדוגמה, \( \left(1,1\right)+\left(1,0\right)=\left(0,1\right) \). כבר לחבורה הפשוטה יחסית הזו יש שימושים מגניבים - הנה דוגמה. היא אפילו זוכה לשם משלה - “חבורת קליין”, על שם המתמטיקאי פליקס קליין שאמנם התעסק איתה אבל גם עם המון דברים אחרים בתורת החבורות ואיכשהו יצא שהשם שלו מתקשר לתורת החבורות דווקא בגללה.

הסימון \( \mathbb{Z}_{2}\times\mathbb{Z}_{2} \) רומז שאיכשהו “בניתי” את החבורה בעזרת \( \mathbb{Z}_{2} \). זה נכון - ביצעתי כאן בניה שנקראת מכפלה ישרה, אבל עוד לא אציג אותה במפורש. הנקודה הרלוונטית פה היא שקל יחסית להבין חבורה אם מבינים איך היא “מורכבת” מחבורות פשוטות יותר. זה משמעותית יותר נוח מטבלאות כפל למיניהן.

ומה יקרה עם טבלת כפל עבור חמישה איברים? עבור ארבעה איברים כבר קיבלנו שתי חבורות שונות, ולכן עבור חמישה איברים אפשר לקוות לעוד יותר, כי יש יותר חופש בחירה. אני מציע לכם לשחק את המשחק ולנסות לראות מה תקבלו. בוודאי שתקבלו את \( \mathbb{Z}_{5} \), אבל האם תגלו משהו שונה מהותית? האם תצליחו למלא טבלת כפל שבה יש איבר שונה מ-\( e \) שכאשר הוא מוכפל בעצמו מתקבל \( e \), כמו בחבורת קליין? אל תנסו לעבור על כל האפשרויות כי יש המון ומהר מאוד תגלו כמה לא נוחה היא כל גישת טבלת הכפל הזו, אבל תנו נסיון כלשהו ותראו מה קורה - לא משנה כמה תתחכמו, אתם תפסידו בסודוקו הזה ולא תצליחו לייצר חבורה כזו. כי פשוט חבורה שכזו לא קיימת; יש רק חבורה אחת עם 5 איברים והיא \( \mathbb{Z}_{5} \). למה זה נכון? נראה את זה בפוסט הבא, שבו נציג גישות קצת יותר חכמות להתמודדות עם הקטע הזה של לנסות להבין איך להציג חבורה ומה המבנה שלה.