איך חישב ארטוסתנס את היקף כדור הארץ

יום אחד, לפני אלפיים ומשהו שנים, קם אדם בבוקר והחליט שהופס - היום הוא ימדוד את היקף כדור הארץ. הלך כמה צעדים, עמד בשמש, מדד איזה צל שהיה בסביבה, עשה עוד איזה חישוב - וסיים! הוא חישב את היקף כדור הארץ, ברמת דיוק טובה למדי. בלי לצאת למסע שמקיף את כל כדור הארץ. בלי תמונות לווין. בלי תקשורת לצד השני של הכדור. לאדם הזה קראו ארטוסתנס והוא היה מתמטיקאי (בין היתר, הוא עשה עוד כל מני דברים) יווני. איך בדיוק הוא עשה את הקסם המדהים הזה? ובכן, מתמטיקה זה מגניב. אחרי הפוסט הזה אני מקווה שגם אתם תדעו.

כמובן, ההצגה בפסקה הקודמת של הסיפור היא נאיבית במתכוון. הפרטים המדוייקים מראים שארטוסתנס התכונן לעניין וידע בדיוק מתי למדוד ואת מה. וגם היה לו קצת מזל של להיות במדינה הנכונה.

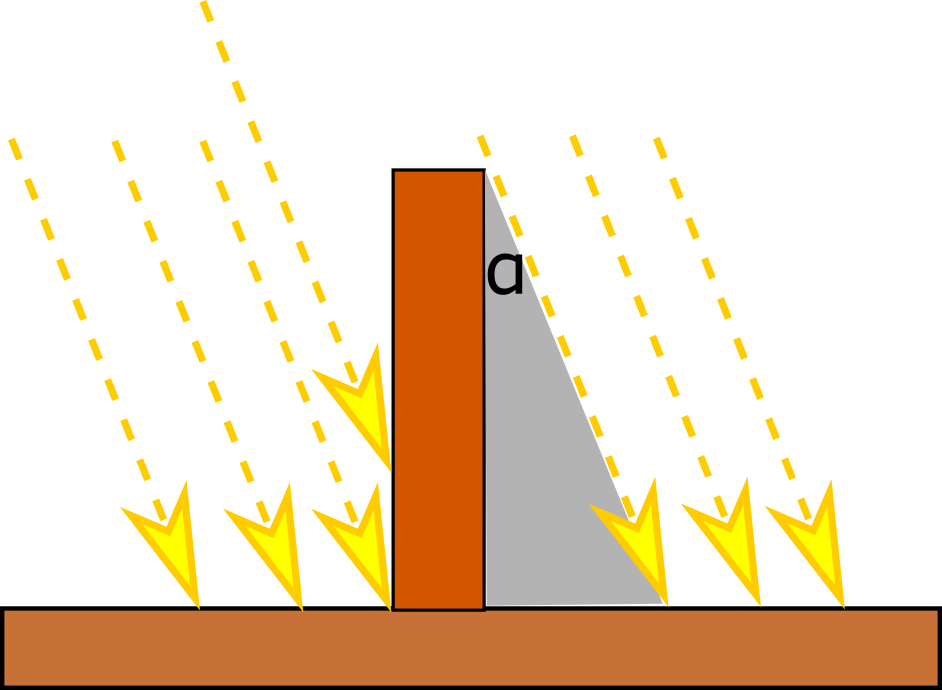
אז בואו נדבר קצת על ארטוסתנס ומה שהוא ידע ועזר לו בחישובים. ארטוסתנס עצמו חי את רוב חייו באלכסנדריה, שהייתה אז אחד ממרכזי התרבות העולמיים, והוא שימש בתפקיד הספרן הראשי של הספריה של אלכסנדריה, שזה קצת כמו להיות הממונה על האינטרנט בימינו. אלכסנדריה ממוקמת בצפון מצרים; בדרום הייתה העיר שבתנ”ך נקראת סונה (באנגלית Syene) והיום נקראת אסוואן. לסונה הייתה תכונה מעניינת מאוד: ביום של נקודת ההיפוך של הקיץ (“היום הארוך ביותר בשנה”, 21 ביוני), באמצע הצהריים, השמש זרחה הישר מעל העיר. דהיינו, הקרניים מהשמש הגיעו בקו ישר ובשעה הזו לא היה צל כלל. הסיפור מספר על באר עמוקה שבשעה הזו השמש האירה רק את תחתיתה, לא את הצדדים. בפועל, כמובן שזה לא היה מדויק לחלוטין - הקרניים כן הגיעו בזווית כלשהי, פשוט קטנה מאוד, מה שלא יכל לקלקל יותר מדי את החישוב. בציור כאן אנחנו רואים מימין מה קרה בדרך כלל, ובשמאל מה קרה במועד המיוחד.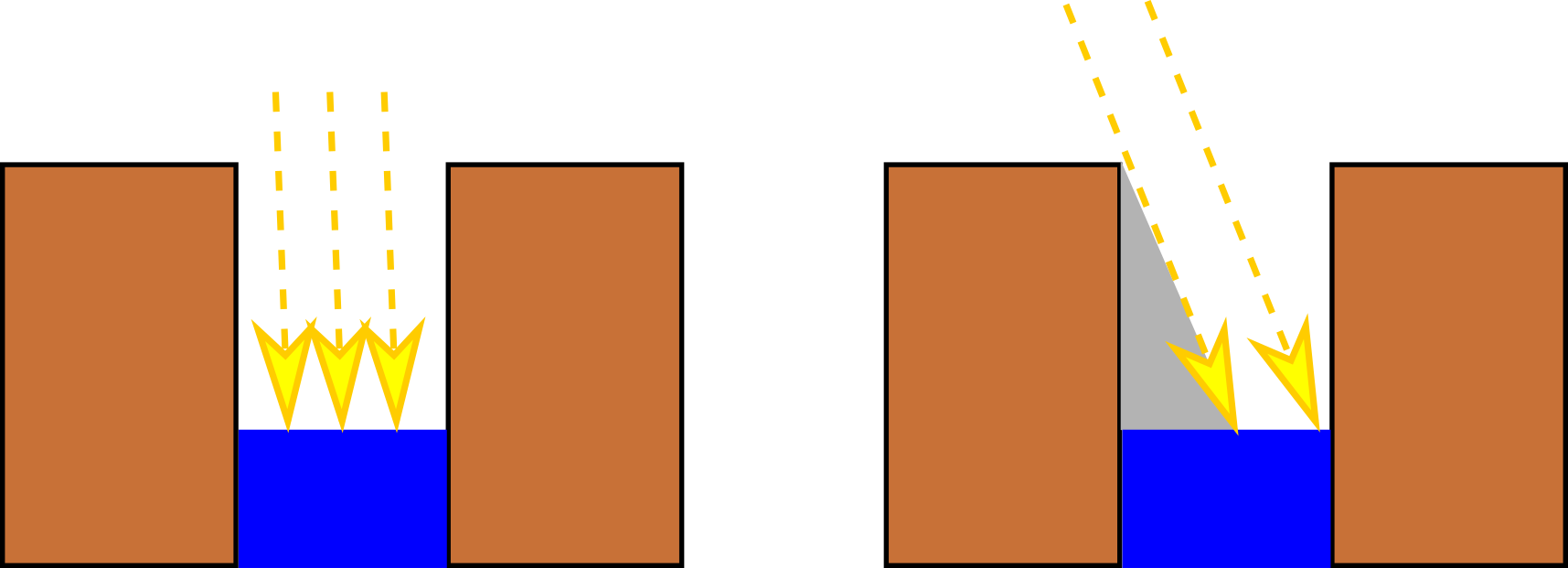

ארטוסתנס ידע גם שבאלכסנדריה זה לא המצב - באותו היום ובאותה השעה, השמש כן הטילה צל. מה גורם להבדל? בהנחה שהקרניים מהשמש שמגיעות לכדור הארץ כולן מקבילות זו לזו, פירוש הדבר הוא שהארץ אינה שטוחה אלא מעוקלת קצת. הרעיון הגאוני של ארטוסתנס היה שאפשר יהיה ללמוד משהו על כמה הארץ מעוקלת על ידי כך שמודדים את הזווית שבה קרני השמש מגיעות לאלכסנדריה באותו הזמן שבו הן מגיעות לסונה באופן ישיר. עוד רגע נסביר איך בדיוק ונראה ציורים.

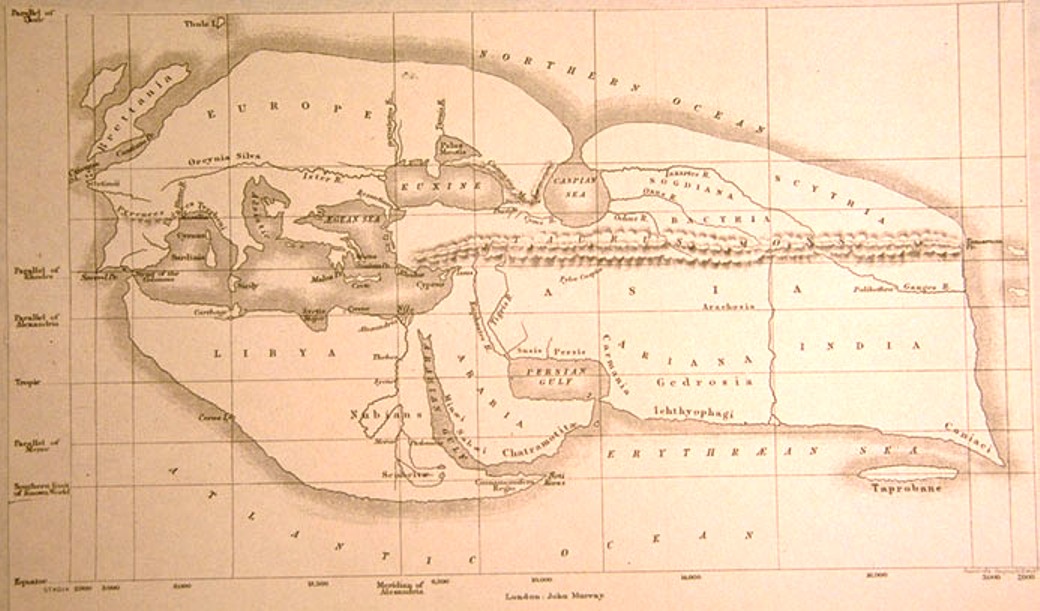
לארטוסתנס היה עוד מידע - הוא ידע (בערך) מה המרחק בין אלכסנדריה לסונה. זה כל המידע הנוסף שהוא נזקק לו. בנוסף לכך, הוא הניח שהארץ היא כדור מושלם. בפועל הארץ אינה כדור מושלם, ומדידת המרחק בין אלכסנדריה לסונה לא הייתה מושלמת, ואלכסנדריה וסונה נמצאות רק בערך על אותו קו אורך כך ששעת הצהריים בהם לא הייתה זהה לחלוטין, כך שהחישוב לא היה מושלם. הטעות הייתה בין 10 ל-15 אחוז (עוד מעט נסביר למה אנחנו לא בטוחים מה הייתה הטעות). תחשבו על זה שניה. זו טעות כמעט זניחה. בעולם של לפני אלפיים שנה, עולם שבו במפה שהכין ארטוסתנס עצמו (ואני מציג שחזור שלה למטה) לא הכירו את אמריקה, אוסטרליה, צפון אירופה וכמעט כל אסיה, בא איש ומודד צל ומקבל הערכה מצויינת לרדיוס כדור הארץ. קסם! כריסטופר קולומבוס קרא את ארטוסתנס, לא האמין, וסבר שהיקף כדור הארץ קטן בשליש ממה שארטוסתנס אמר. כתוצאה מכך הוא חשב שיש לו סיכוי להגיע להודו אם ייסע מערבה מאירופה, ולא הבין שהיבשת שהגיע אליה איננה הודו. אם היה מקשיב לארטוסתנס היה יודע. אולי (תיאוריה אחרת ששמעתי היא שקולומבוס חשב שהודו גדולה בהרבה ממה שהיא באמת).

בואו נעבור עכשיו לפרטים של מה ארטוסתנס עשה. הוא חיכה לצהריים ביום נקודת ההיפוך של הקיץ, ואז הלך אל מגדל גבוה שהיה באלכסנדריה, והטיל צל - שהרי השמש באלכסנדריה לא הייתה בדיוק מלמעלה, והקרניים הגיעו בזווית. הוא ידע את גובה המגדל וחישב את אורך הצל שעל הקרקע, ומזה הוא חישב את הזווית שבה הקרניים הגיעו (כלומר, כמה באיזה סיבוב הן ביחס לקרן שמגיעה במאונך, כמו בסונה). איך הוא חישב? שאלה טובה, לא מצאתי פירוט לזה במקורות שקראתי, אבל בזמנו של ארטוסתנס הטריגונומטריה הייתה קיימת כבר; אם אורך הצל הוא \( A \) וגובה המגדל הוא \( B \), והזווית המבוקשת היא \( \alpha \), אז מתקיים הקשר הפשוט \( \tan\alpha=\frac{A}{B} \). קרוב לודאי שהייתה לו כבר טבלה עם נתונים מספריים מקורבים; הזווית שהוא מצא היא \( 7.2 \) מעלות, כלומר, 360 מעלות (מעגל שלם) חלקי 50. זה טיפה עגול מדי; מן הסתם החישוב פה היה מקורב (הנה לנו עוד קירוב שלא השפיע מהותית על התוצאה).

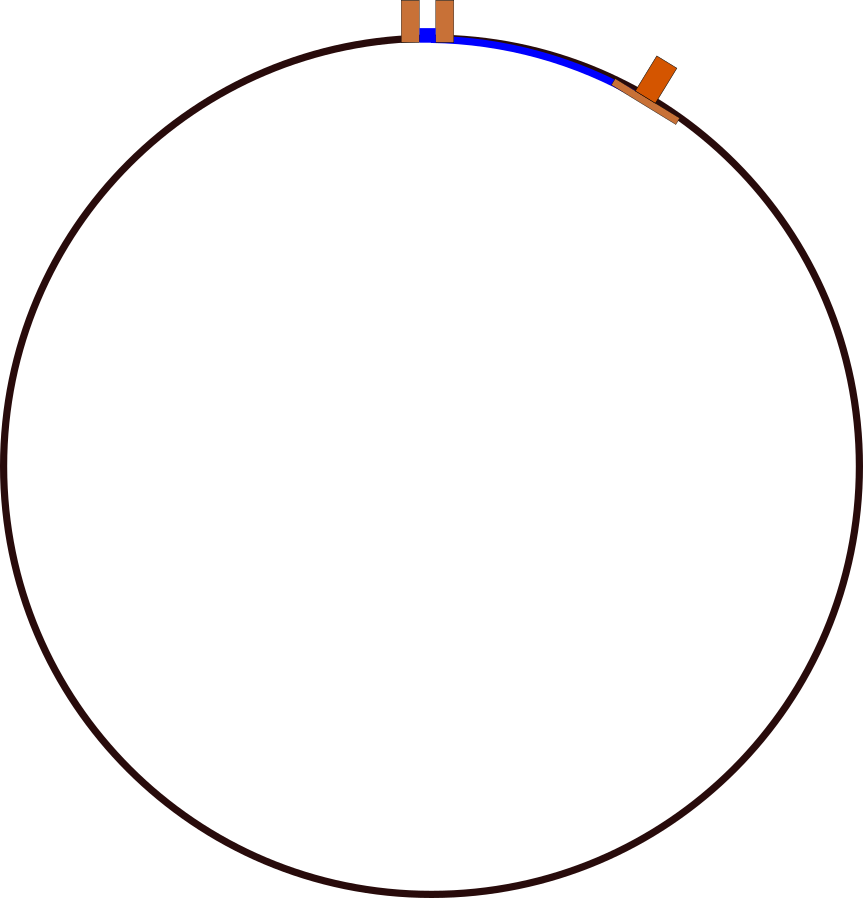
עכשיו מגיע החלק המסובך (יחסית) בכל העסק. בואו ניקח את הקו (על פני כדור הארץ; זה “קו” עקום) הקצר ביותר שמחבר את אלכסנדריה עם סונה, ונמשיך אותו כך שיקיף את כדור הארץ ויתחבר שוב אל סונה. קיבלנו את מה שנקרא “מעגל גדול”. ההיקף שלו הוא היקף כדור הארץ. כעת אפשר לשכוח מכך שהארץ היא כדור ולהסתכל רק על המעגל הדו-ממדי הזה - אם נחשב את ההיקף שלו, סיימנו. ככה זה נראה:

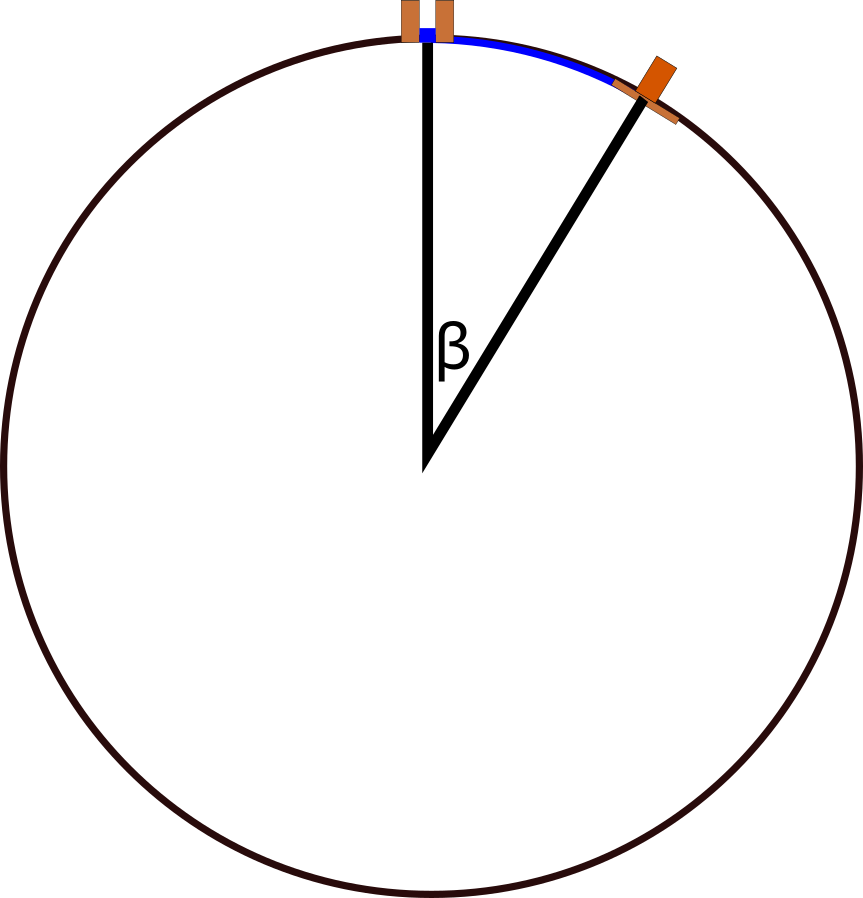
עכשיו, נניח שאנחנו מותחים קווים ישרים שמחברים את סונה ואת אלכסנדריה עם מרכז כדור הארץ ונסמן את הזווית בנקודת החיבור שלהם בתור \( \beta \). מה קיבלנו? שהקו שמחבר את סונה ואלכסנדריה הוא קשת על מעגל, שנשענת על זווית בגודל \( \beta \). אם נמצא כמה פעמים \( \beta \) נכנסת במעגל שלם, ונכפול את אורך הקשת במספר הזה, נקבל את היקף כדור הארץ. דוגמה פשוטה: אם הקשת שלנו נשענת על זווית של 90 מעלות, הרי שהיא תופסת בדיוק רבע מהמעגל, ולכן צריך לכפול את אורך הקשת ב-4 כדי לקבל את ההיקף.

כפי שבוודאי כבר ניחשתם, אפשר להראות (ותכף נעשה את זה) ש-\( \beta \) היא אותה \( \alpha \) שארטוסתנס מדד. כלומר, על פי הקירוב של ארטוסתנס, היקף כדור הארץ הוא בערך 50 כפול המרחק בין סונה ואלכסנדריה. מה המרחק הזה? פתחתי את Google maps, השתמשתי בכלי מדידת המרחק שלהם, ראיתי שהמרחק בין אלכסנדריה ואסוואן (סונה של ימינו) הוא בערך (שוב ה”בערך” הזה?!) 840 ק”מ, וכפול 50 מקבלים שהיקף כדור הארץ הוא 42,000 ק”מ. היקף כדור הארץ האמיתי הוא 40,075 ק”מ. כלומר, קיבלנו היקף שהוא 104 אחוז מההיקף האמיתי - שגיאה של 4 אחוז. שמעו, זה ממש מוצלח! קיבלנו קירוב ממש טוב, בהתחשב בכך שאנחנו בכלל לא מתייחסים לעובדה שכדור הארץ הוא בכלל לא כדור אלא אליפסואיד.

כמובן, לנו קל. אנחנו פשוט פותחים גוגל ומקבלים את המרחק בין שתי הערים. אצל ארטוסתנס זה לא היה ככה. איך באמת מדדו מרחקים? בדקו כמה זמן (נטו, רק כשנמצאים בתנועה) לוקח להגיע מעיר אחת לשניה. אני מניח שגם ניסו להעריך את המהירות בהתחשב בתנאי הדרך. אני מודה שאין לי מושג מה עשו באמת; ההיסטוריה של המדע היא מרתקת למדי. מכל מקום, יחידת המרחק שארטוסתנס השתמש בה נקראת סטדיה (או לפעמים סטדיון) והבעיה היא שאין לנו ודאות מהי היחידה הזו במונחים מודרניים. יש רק הערכות שונות ומשונות, שמן הסתם נותנות הערכות שונות למרחק בין סונה ואלכסנדריה. ארטוסתנס דיבר על מרחק של 5,000 סטדיות (עגול מדי!!!!! קירוב!), ועל פי הערכה אפשרית אחת, סטדיה הייתה 176 מטרים, מה שנותן לנו היקף של 44,100 ק”מ - שגיאה של 10 אחוז. הערכות אחרות לסטדיה נותנות שגיאות גדולות יותר, אבל לא משמעותית. כמובן, זה החלק המעניין פחות בסיפור הזה כי ארטוסתנס לא חישב את המרחק בעצמו; המדידות שהוא עצמו ביצע, והטכניקה שבה השתמש, כשהן מופעלות על הנתון המדוייק של המרחק, נותנות, כפי שראינו, קירוב מצויין.

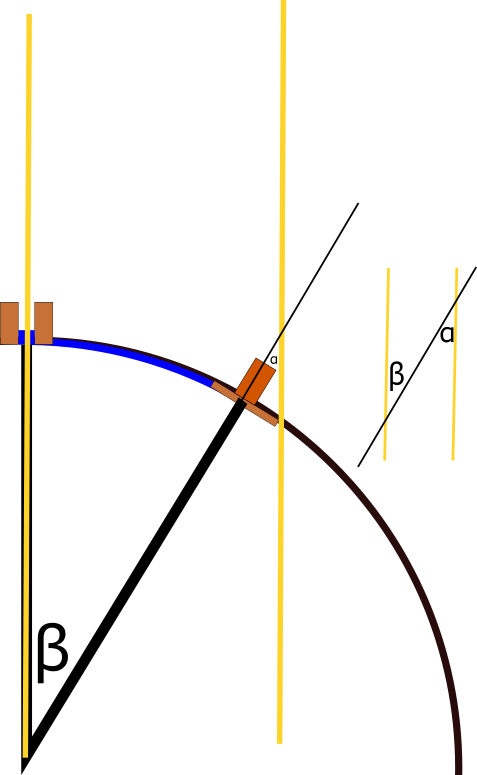
נשאר רק להסביר איך הזווית שעליה נשענת הקשת אלכסנדריה-סונה יוצאת זהה לזווית של הצל שהשמש הטילה על אלכסנדריה כשהיא הייתה הישר מעל סונה. את זה עושים עם גאומטריה אוקלידית בסיסית מהסוג שרואים בבית הספר. נתחיל עם האיור.

באיור הזה אפשר לראות שני קרני שמש מקבילות שמגיעות לכדור הארץ - האחת אל סונה, הישר מלמעלה; והשני אל אלכסנדריה, בזווית. אם מסתכלים ממש טוב אפשר לראות שסימנתי את הזווית הזו ב-\( \alpha \) כמו בתמונה שהייתה קודם עם המגדל. בצד ציירתי גרסה מופשטת של הסיפור הזה. אנחנו רואים ש-\( \alpha,\beta \) הן מה שמכונה “זוויות מתחלפות”. אלו שתי זוויות שנוצרות כאשר קו חותך שני ישרים מקבילים, שתי הזוויות נמצאות בצדדים שונים של המקבילים (אצלנו \( \alpha \) משמאל לקו המקביל שאליו היא צמודה ואילו \( \beta \) מימין), ובצדדים שונים ביחס לקו החותך (כאן \( \alpha \) מתחתיו ואילו \( \beta \)מעליו). במקרה כזה, אפשר להוכיח ששתי הזווית שוות, מה שכמובן מסיים את הכל.

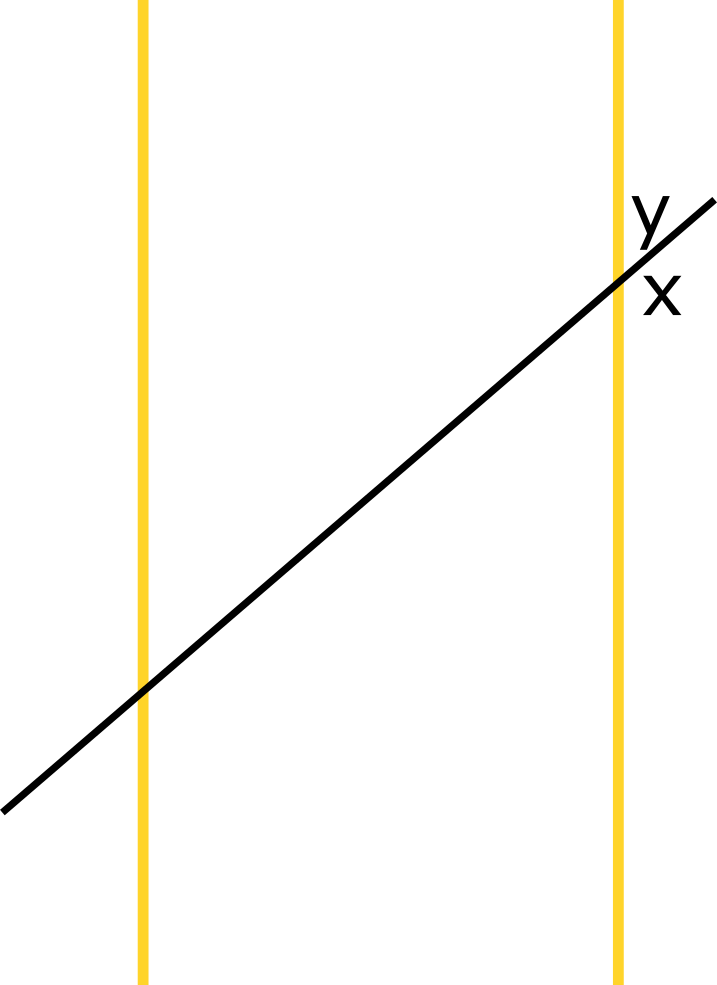
רגע, למה לא להסביר לכם על הדרך גם איך מוכיחים את זה? הנה איור כללי קצת יותר:

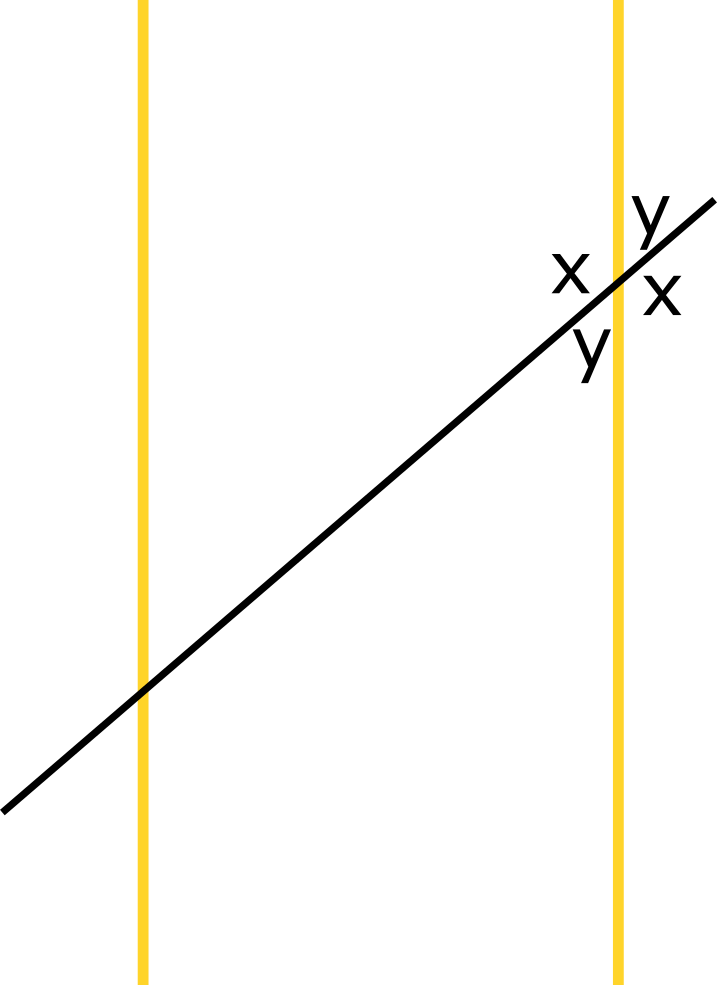
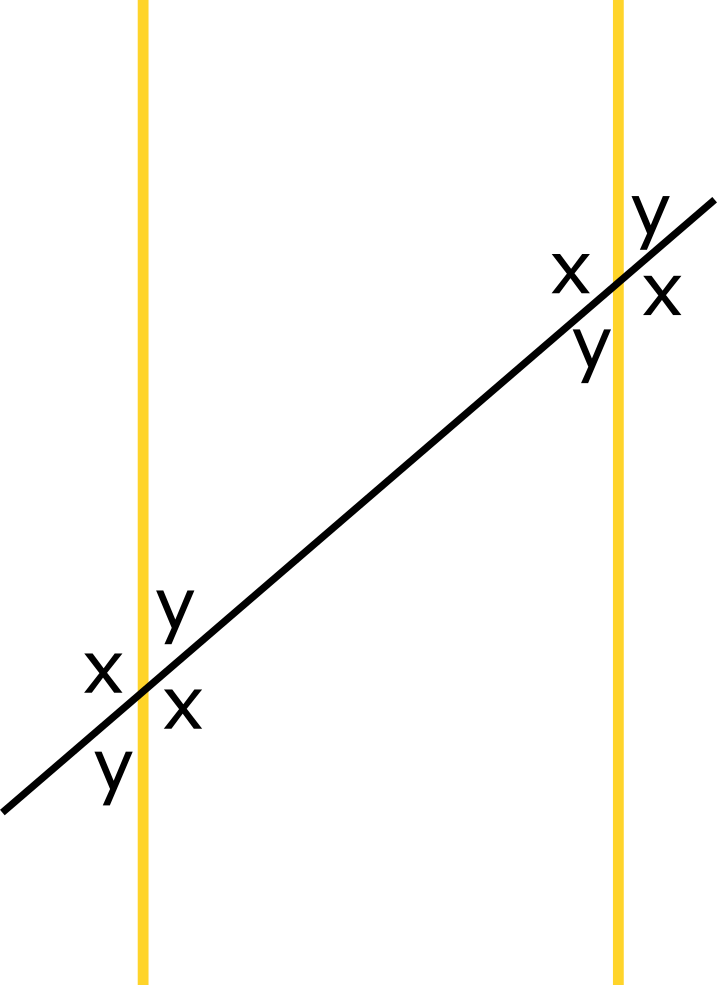
כאן לקחתי את שני המקבילים (הצהובים) ואת הקו שחותך אותם (השחור). יש לנו שמונה זוויות, ואנחנו רוצים לדעת מי מהן שוות ומה אפשר להגיד על היתר. אנחנו הולכים להתבסס ללא הוכחה על שני דברים של אוקלידס. האחד (טענה 13 בספר 1 של “יסודות”), שאם יש לנו קו ישר \( A \), וקו אחר \( B \) שחותך אותו, ואנחנו מסתכלים על סכום שתי הזוויות שנמצאות באותו צד של \( A \) ונוצרות על ידי החיתוך עם \( B \), אז הסכום של שתי הזוויות הללו הוא 180 מעלות בדיוק (מה שאוקלידס מכנה “שתי זוויות ישרות”). בואו נקרא לקו הצהוב הימני \( A \), לקו השחור \( B \), ונסתכל על שתי הזוויות שבצד ימין של הקו. נקרא להן \( x,y \). אז קיבלנו מהמשפט של אוקלידס ש-\( x+y=180 \). עכשיו בואו “נחליף דיסקט” ונחשוב על \( A \) דווקא בתור הקו השחור, על הצהוב הימני בתור \( B \) ונסתכל על שתי הזווית שמעל הקו השחור. אחת מהן אנחנו כבר מכירים ה-\( y \) הימנית. את השניה אנחנו לא מכירים אבל אנחנו יודעים שסכומה עם \( y \) הוא 180, כלומר היא שווה ל-\( 180-y \) ולכן ל-\( x \). בצורה דומה מראים שהזווית הנותרת שלא טיפלנו בה היא \( y \). מה שעשינו פה הוא בעצם להוכיח את המשפט לפיו זוויות קודקודיות הן שוות (כשחותכים ישר עם ישר אחר נוצרות ארבע זוויות; זוג זוויות הן קודקודיות אם הן לא נוגעות זו בזו מלבד בנקודת החיתוך של הישרים).

עכשיו, בואו נדבר על המקביל השני. גם לו יש ארבע זוויות שאפשר לחלק לשני זוגות שווים בואו ניתן להם שמות: \( a,b \).

איך נוכל להגיד משהו על הקשר בין \( x,y \) ובין \( a,b \)? כאן אוקלידס נזקק לאקסיומה: הוא טוען שאם שני ישרים הם מקבילים, ואם נסתכל על ישר שחותך את שני הישרים הללו, וניקח שתי זוויות שהן מצדדים שונים של המקבילים אבל מאותו צד של הישר החותך, אז סכום הזוויות הזה גדול או שווה ל-180. ליתר דיוק, הניסוח המדויק של אוקלידס הוא שקול, אבל מוצג הפוך. אם נגיד “אם יורד גשם אז יש עננים בשמיים” זה שקול לכך שנגיד “אם אין עננים בשמיים אז לא יורד גשם” - מה שעשינו פה היה להוסיף “לא” לשתי הטענות ולהפוך את כיוון הגרירה שלהן. אצל אוקלידס, אם כן, הטענה היא “אם יש לנו שני ישרים שנחתכים על ידי ישר שלישי, ואנחנו לוקחים זוויות מצדדים שונים של הישרים ומאותו צד של הישר השלישי ורואים שסכומן קטן מ-180, אז הישרים נפגשים מתישהו”.

המשפט המסורבל והמפותל הזה נקרא אקסיומת המקבילים והיא ראויה לפוסט מיוחד שעוסק בהיסטוריה המרתקת שלה, שמתקשרת למה שנקרא גאומטריות לא אוקלידיות. אבל שולי הפוסט הזה צרים מלהכיל את כל הסיפור הזה. רק אעיר שזה הניסוח המקורי של אוקלידס; ניסוח שקול מודרני ופופולרי יותר הוא “לכל ישר ונקודה מחוץ לישר ניתן להעביר מקביל אחד ויחיד לישר שעובר דרך הנקודה”. דווקא הניסוח המקורי של אוקלידס יותר עוזר לנו כאן.

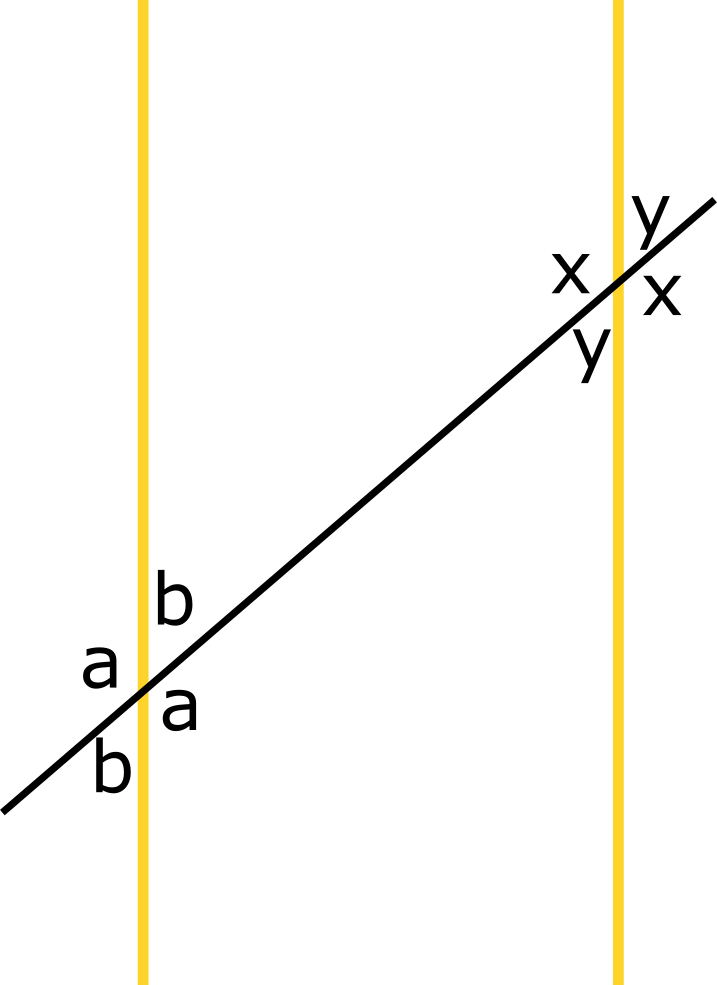
עכשיו, במקרה שלנו יש שני זוגות של זוויות שהן מצדדים שונים של המקבילים ומאותו צד של הישר השלישי: במקרה הראשון אלו \( x,b \) ובמקרה השני אלו \( y,a \). מה שראינו בהתחלה, מטענה 13, הוא ש-

\( x+y=180 \)

\( a+b=180 \)

ומה שאקסיומת המקבילים מספרת לנו הוא ש-

\( x+b\ge180 \)

\( y+a\ge180 \)

חיבור שתי המשוואות הראשונות נותן לנו \( x+y+a+b=360 \). מצד שני, אם \( x+y>180 \) או אם \( y+a>180 \), אז מחיבור שתי המשוואות נקבל \( x+y+a+b>360 \) וזו סתירה. לכן בהכרח קיבלנו \( x+b=180 \) ו-\( y+a=180 \). על כן, \( a=180-y=x \) ו-\( b=180-x=y \):

וזה משלים את ההוכחה.

לסיום, הערה אישית: ראיתי את השיטה של ארטוסתנס לראשונה בבית הספר התיכון והתלהבתי מאוד. רק מה, לא ראיתי אותה בשיעור מתמטיקה; ראיתי אותה בשיעור פיזיקה, בגלל שהמורה (כתבתי בטעות “מרצה” בהתחלה, דווקא מתאים) נהג באופן כללי להגדיל ראש ולהראות לנו דברים מגניבים. זו לגמרי תוצאה שכדאי להראות בבית הספר. אין סיבה שלא. המתמטיקה פה, כפי שראיתם, היא טריגונומטריה בסיסית ביותר וגאומטריה אוקלידית שממילא יודעים. יש כאן תשובה מצויינת ל”בשביל מה זה טוב”, יש כאן רעיון מגניב שאפשר לבצע בפועל, ויש כאן המחשה נאה לאופן שבו כבר בתקופת היוונים לא רק שהבינו שהעולם הוא בקירוב כדור (לא, לא היה צריך את קולומבוס בשביל זה) אלא גם שידעו להגיד עליו דברים מאוד לא טריוויאליים. אני מקווה שזה בדיוק מסוג הדברים שיאפשר לאנשים לראות כמה מתמטיקה יכולה להיות מגניבה, גם בלי להיכנס לעומק.