מעגלים בוליאניים - מה זה בכלל?

אני מתחיל את פרוייקט “תוצאות מפתיעות בסיבוכיות” עם תיאור של משפט ברינגטון, שכמו רוב המשפטים בסיבוכיות הוא יחסי - אומר ששתי מחלקות סיבוכיות בעלות הגדרה שונה הן זהות - ועל כן נשמע לקורא מבחוץ כמו “ג’יבריש ג’יבריש בלה בלה שווה לבלה בלה ג’יבריש ג’יבריש”. אין מנוס, לפני שמציגים את המשפט, להציג את מחלקות הסיבוכיות המתאימות ולמה הן מעניינות. מילת אזהרה כללית: למרות שאני מייעד את הפוסטים הללו לכל קוראי הבלוג, אני בהחלט עשוי לזרוק פה ושם מושגים שנראים לי ברורים ולקורא לא. במקרה כזה אפשר לשאול שאלה בתגובות, אפשר לחפש בפוסטים ישנים יותר בבלוג, ואפילו להיעזר בויקיפדיה.

באופן כללי, מחלקת סיבוכיות היא אוסף של פונקציות שניתן לחשב בעזרת מודל חישובי מסויים שעל כמות המשאבים שלו יש מגבלה כלשהי. המודל הקלאסי נקרא מכונת טיורינג והמגבלה הקלאסית עליו היא זמן ריצה פולינומי (שניתן לחסום על ידי פולינום). אנחנו לא הולכים לדבר על המודל הזה. הפעם אני הולך לדבר על מודל שונה למדי - מעגלים בוליאניים (Boolean Circuits).

ראשית, המטרה שלנו. אנחנו הולכים לדבר רק על פונקציות בוליאניות - כאלו שמקבלות קלט שהוא סדרה של 0 ו-1, ומוציאות פלט שהוא ביט בודד - או 0 או 1. פורמלית, \( f:\left\{ 0,1\right\} ^{n}\to\left\{ 0,1\right\} \). בהקשר של מדעי המחשב מספיק לדבר על פונקציות כאלו כי כל פונקציה אחרת שניתן לחשב במחשב ניתנת לתיאור באמצעות פונקציות בוליאניות. על ערכים בוליאניים אוהבים להגדיר פעולות של “וגם” ו”או”, מתוך מחשבה על ערך 1 כמייצג “אמת” וערך 0 כמייצג “שקר”. אם \( x,y \) הם שני ביטים, אז \( x\wedge y \) (\( x \) וגם \( y \)) הוא 1 אם ורק אם \( x=y=1 \), אחרת הוא 0; ואילו \( x\vee y \) (\( x \) או \( y \)) הוא 0 אם ורק אם \( x=y=0 \) ואחרת הוא 1. ה”או” הזה קצת שונה מהמשמעות שלו בחיי היום יום, כי הוא יכול לקבל “אמת” גם אם שני המשתנים קיבלו “אמת” (“או שאלך לים או שאקרא ספר” נשמע כאילו הוא אומר “אעשה אחד משני אלו אך לא את שניהם בו זמנית”). יש אופרטור אחר, Exclusive Or, או בשמו המקוצר XOR, ובסימון \( x\oplus y \), שמקבל 1 אם ורק אם בדיוק אחד משני המשתנים מכיל 1, שממדל את ה”או” היומיומי. כמו כן יש אופרטור שלילה שפועל רק על משתנה יחיד: \( \neg x \) הוא 1 אם ורק אם \( x \) היה 0.

אלו פונקציות בסיסיות, אבל אפשר להגדיר פונקציות מורכבות יותר על הרבה יותר ביטים. החל ממשהו מטופש כמו \( f\left(x_{1},\dots,x_{n}\right)=\bigwedge x_{i} \) שמקבל 1 אם ורק אם כל \( n \) הקלטים הם 1, עבור בדברים יותר מתוחכמים כמו \( \mbox{MAJORITY}\left(x_{1},\dots,x_{n}\right) \) שמקבלת 1 אם ורק אם רוב הביטים בקלט הם 1, וכלה בדברים ממש מתוחכמים כמו הפונקציה שמוציאה 1 רק אם הביטים של הקלט שלה, כשמפרשים אותם על ידי קידוד כלשהו בתור גרף, מייצגים גרף שמכיל מעגל המילטוני. למעשה, אפשר לכמת ולהגיד בדיוק כמה פונקציות יש מ-\( n \) ביטים אל שני ביטים: \( 2^{2^{n}} \). כבר עבור ערכים לא גדולים של \( n \) המספר הזה הוא עצום - יש עושר רב של פונקציות בינאריות. השאלה שאנו שואלים את עצמנו היא - אילו פונקציות ניתן לתאר באמצעות שימוש בפונקציות בסיסיות ופשוטות בלבד, ובאופן חסכוני במשאבים?

כאן נכנסים המעגלים הבוליאניים לתמונה. ההשראה לשימוש בהם בתורת הסיבוכיות הכל כך תיאורטית הגיעה ישירות מהשימוש בהם כדי לתאר (מודל מופשט של) חומרה. שערים לוגיים הם הבסיס למחשב אמיתי; אם כן, למה לא להשתמש בהם כדי לתאר חישובים? כתמיד בתורת הסיבוכיות, צריך לזכור מה המטרה שלנו. היא איננה להציג מעגלים לחישוב של כל מני פונקציות מגניבות - כשמדעני מחשב מנסים לפתור בעיה הם עושים את זה תמיד במודל מופשט ככל העניין, ורק בסוף מתחילים לשאול את עצמם האם ניתן “לתרגם” את הפתרון למודלים פשוטים וקונקרטיים יותר - המטרה היא בדיוק ההפך, להראות שאי אפשר לפתור בעיות מסויימות. שהמודל של מעגלים בוליאניים הוא חלש במידה מסויימת, וכפועל יוצא מכך - שיש בעיות שהן קשות אינהרנטית, ובאף מודל מציאותי לא ניתן יהיה לפתור אותן. בתחילת שנות השבעים, שהמעגלים הבוליאניים נכנסו לתמונה כמודל חישוב אלטרנטיבי למודל הסטנדרטי של מכונת טיורינג, התקווה הייתה שבגלל הפשטות הרבה שלהם והאופי הקונקרטי יותר שלהם, יהיה קל יותר להוכיח חסמים תחתונים עבורם מאשר עבור מכונת טיורינג. התקווה הזו התבדתה למדי במהלך השנים כשהתברר עד כמה הוכחת חסמים תחתונים אפילו עבור המודל הזה היא קשה. תוצאה מפורסמת ביותר בהקשר הזה היא זו של רזבורוב ורודיץ’ מ-94, שהראתה כי “הוכחות טבעיות” (לא אכנס כרגע להסבר של המושג) לא מסוגלות להוכיח חסמים תחתונים עבור מעגלים בוליאניים. ובניסוח יומיומי: יש הוכחה מתמטית לכך שיהיה מאוד, מאוד קשה להוכיח חסמים תחתונים על מעגלים בוליאניים. מכיוון שאחד מהיעדים הבסיסיים של חסמים תחתונים על מעגלים בוליאניים הוא להוכיח ש-\( \mbox{P}\ne\mbox{NP} \), זוהי עוד דוגמה לכך ששאלת \( \mbox{P}\ne\mbox{NP} \) היא שאלה קשה בצורה יוצאת דופן, וגם פתרונה כנראה יצטרך להיות יוצא דופן - גישה שונה לגמרי למושג הסיבוכיות ולאופן שבו מוכיחים חסמים תחתונים לגביו.

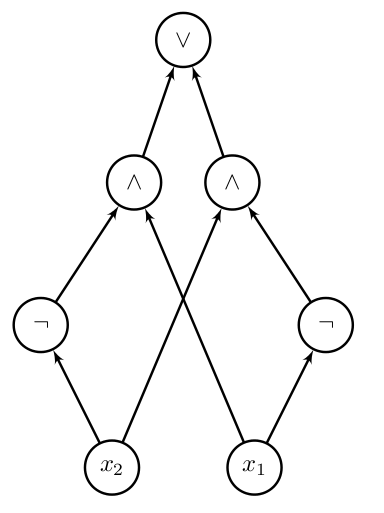
בואו נעבור להגדרה של מעגל בוליאני - מה זה בכלל? כרגיל בעניינים כאלו, תמונה אחת שווה אלף מילים:

פורמלית, מעגל בוליאני הוא גרף מכוון וחסר מעגלים (מהו המושג הזה? יש לי פוסטים על גרפים, אבל אני מקווה שגם מבט בתמונה מספיק כדי להבהיר את זה), שכל צומת “כניסה” שלו (צומת שאין קשתות שנכנסות אליו) מסומן במשתנה, כל צומת פנימי שלו מסומן ב-\( \wedge \) או ב-\( \vee \) או ב-\( \neg \), וכל צומת שאין ממנו קשתות יוצאות נחשב צומת פלט. כדי לפשט את העניינים מניחים שיש רק צומת פלט יחיד, אבל רוב מה שמדברים עליו עובד גם עבור מספר צמתי פלט (שמאפשרים לדבר על פונקציות שמוציאות כפלט יותר מביט בודד). לצמתי \( \neg \) יכולה להיכנס רק קשת בודדה, אבל לצמתי \( \wedge \) ו-\( \vee \) יכול להיכנס מספר קשתות כלשהו, אם כי עוד מעט נגיד למה כן צריך להגביל את זה לפעמים.

בהינתן השמה כלשהי למשתנים, כלומר סדרה של 0 ו-1 לכל אחד מהמשתנים שבצמתי הכניסה של המעגל, הערך של צומת הפלט נקבע באופן הבא: כל צומת שטרם קבענו את ערכו אבל כן קבענו את ערכם של כל הבנים שלו - הצמתים שיש קשת מהם אליו - הערך שלו מחושב בהתאם לערך הבנים ולסימן שלו. למשל, צומת שמסומן ב-\( \wedge \) מקבל את הערך 1 אם ורק אם כל בניו קיבלו 1, ואחרת הוא מקבל 0. זה הכל. פלט המעגל על ההשמה הוא ערך של צומת הפלט. בדרך כלל מסמנים מעגל ב-\( C \) ואת הערך שלו על השמה מסויימת \( x \) ב-\( C\left(x\right) \) (כאן צריך לחשוב על \( x \) כעל מחרוזת ביטים שאורכה כמספר המשתנים של המעגל).

עכשיו משהמודל הבסיסי הובהר, הגיע הזמן להניח את הקלפים על השולחן ולהתייחס לאספקט שבמבט ראשון נראה מוזר ובעייתי של מעגלים, אל מול מכונות טיורינג. מכונת טיורינג היא מה שנקרא “מודל חישוב יוניפורמי” (למה “יוניפורמי” ולא המילה העברית הנאה “אחיד”? אין לי תשובה טובה יותר מ”ככה”). המשמעות של יוניפורמיות כאן היא שאותה המכונה מתמודדת עם קלטים מכל גודל שהוא. אין לי בעיה לבנות מכונת טיורינג בודדת לחישוב הפונקציה \( \mbox{MAJORITY} \) שהזכרתי קודם, והיא תדע להתמודד עם קלטים מגודל \( n \) לכל \( n \) טבעי שרק תרצו. לעומת זאת, מעגל בוליאני בנוי מראש עבור \( n \) ספציפי; עבור \( n \)-ים אחרים נזדקק למעגלים אחרים. אולי כולם ייראו דומים אחד לשני, אבל הם לא יהיו אותו מעגל - בפרט, הגודל שלהם יהיה שונה (ולו רק בגלל שיצטרכו להיות בהם יותר צמתי קלט).

אפשר היה לעקוף את הקושי הזה ולהגיד שמראש אנחנו רוצים לדבר רק על \( n \) קונקרטי אחד וחסל. אלא מה, כל מהותה של תורת הסיבוכיות הוא לעסוק בחסמים אסימפטוטיים על סיבוכיות - כלומר, לשאול שאלות כמו “עבור \( n \)-ים הולכים וגדלים, כמה מהר יגדל זמן החישוב שנדרש למכונת טיורינג כדי להתמודד עם קלט בגודל \( n \) כשהיא מנסה לחשב את הפונקציה הזו והזו?”. לכן כשמדברים על בעיה חישובית שאנו רוצים לפתור באמצעות מעגלים, אנחנו לא מדברים על פונקציה \( f \) בודדת שאנו רוצים לחשב אלא על משפחת פונקציות \( f_{1},f_{2},\dots,f_{n},\dots \) כאשר \( f_{n} \) היא פונקציה על \( n \) קלטים. מן הסתם בדרך כלל כל הפונקציות \( f_{n} \) הללו יהיו דומות זו לזו באופיין - אבל הן לא זהות, כי מספר הקלטים שלהן שונה. בהתאם לכך, לא ניתן יהיה להציג מעגל בודד שמטפל בכל משפחת הפונקציות, אלא משפחת מעגלים \( C_{1},C_{2},\dots,C_{n},\dots \) כך שהמעגל \( C_{n} \) מחשב את הפונקציה \( f_{n} \). לכאורה זה רעיון פשוט ומובן, ולא ברור למה אני מייחס לו כל כך הרבה חשיבות, עד שמתברר עד כמה החוסר-יוניפורמיות הזה גורם לתופעות מוזרות. הנה הדוגמה הקלאסית לעניין. שפה אונרית היא קבוצה של מילים (מילה, לצורך העניין, היא רצף של ביטים) שכל המילים בה הן סדרה של 1-ים, כלומר 0 לא מופיע בכלל. מה שמאפיין את המילים בשפה, אם כן, הוא רק האורך שלהן. לכל \( n \), אחד משניים: או ש-\( 1^{n} \) (סדרה של \( n \) פעמים 1) מופיע בשפה, או שלא. זה אומר שלכל שפה אונרית קיימת משפחת מעגלים ש”מזהה” אותה (מוציאה 1 על מילים ששייכות לשפה ו-0 על מילים שלא). למה? כי קל לבנות מעגל שמוציא 1 על הקלט \( 1^{n} \) - פשוט מבצעים \( \wedge \) על כל ביטי הקלט. גם קל לבנות מעגל שמוציא \( 0 \) על כל הקלטים - למשל \( x_{1}\wedge\neg x_{1} \). לכן לכל \( n \) קיים מעגל, ומעגל קטן ופשוט שעונה את התשובה הנכונה לכל המילים מאורך \( n \). אבל זה לחלוטין לא המצב עם מכונות טיורינג - קיימות שפות אונרית שמכונת טיורינג לא יכולה לזהות (כלומר, לעצור ולומר “כן” או “לא, בהתאם לשייכות המילה לשפה או לא). זה נובע מכך שבכלל קיימות שפות כלשהן שמכונת טיורינג לא יכולה לזהות, ואפשר לקודד שפות כאלו בעזרת מילים אונריות (איך? תרגיל). בקיצור, המודל הלא-יוניפורמי של מעגלים מסוגל לעשות דברים שמכונת טיורינג לא מסוגלת (זה לא אומר שהוא חזק יותר - אם המעגלים מוגבלים, ונראה דוגמאות להגבלות בקרוב, יהיו דברים שמכונת טיורינג יכולה לעשות ומעגלים לא).

אז איך פותרים את ה”בעיה” הזו? אפשר להצטמצם לדיון על משפחות יוניפורמיות של מעגלים - אלו משפחות מעגלים שאפשר לייצר באופן אלגוריתמי. כלומר, יש מכונת טיורינג שעל קלט \( n \) מייצרת את המעגל \( C_{n} \) המתאים. זה חיש קל פותר אותנו מאנומליות כמו שיש לעיל. עם זאת, לרוב אין צורך ביוניפורמיות הזו ולכן לא טורחים לדרוש אותה. הסיבה לכך היא שאין בעיה עם זה שמעגלים יהיו מסוגלים לקבל שפות שמכונת טיורינג לא, כל עוד השפות המעניינות באמת לא שם. אם ניתן יהיה להוכיח שמעגלים לא מסוגלים לעשות דבר מה, וינבע מכך שגם מכונות טיורינג לא יכולות לעשות זאת, למי אכפת שמעגלים מסוגלים לפתור כמה דברים שמכונות טיורינג לא?

הסיפור לא נגמר כאן - אפשר גם להתאים את המודל של מכונת טיורינג כדי שימדל “חוסר יוניפורמיות” שכזה. המודל המתאים הוא של “מכונות שמקבלות עצה”. על קצה המזלג, הרעיון הוא שלכל מספר טבעי \( n \) תותאם מחרוזת של “עצה” \( a_{n} \), ומכונת טיורינג שמתמודדת עם קלט \( x \) מאורך \( n \) תקבל, פרט ל-\( x \), גם את \( a_{n} \) ותוכל להיעזר בו במהלך החישוב. אם אתם אוהבים את הדברים הללו קחו כמה דקות לחשוב למה השינוי הזה אכן מתאים בול לסיטואציה של מעגלים לא יוניפורמיים (ואם אתם ממש שוחים בחומר, נסו לחשוב איך עניין העצה שונה מעניין הזיהוי-יעיל שמגדיר את \( \mbox{NP} \)). למכונות שמקבלות עצה יש יתרון נוסף, והוא שניתן להשתעשע עם הגודל של העצה ולדרוש עליו חסמים שונים ומשונים ולראות מה מקבלים (למשל, מה אפשר לעשות עם ביט בודד של עצה? די הרבה, מסתבר - בפרט להכריע כל שפה אונרית בשיטה שתיארתי לעיל). בדרך כלל דורשים שגודל העצה יהיה פולינומי ב-\( n \), ולמחלקת השפות שאפשר להכריע עם מכונות שמקבלות עצה וזמן הריצה שלהן הוא פולינומי קוראים \( \mbox{P}/\mbox{poly} \) (מה שמשמאל ללוכסן מייצג את סוג המכונה, ומה שמימין ללוכסן מציין את גודל העצה). זו גם בדיוק מחלקת השפות שאפשר להכריע עם מעגלים בוליאניים שגודלם פולינומי ב-\( n \), ולכן השם המוזר והלכאורה לא קשור \( \mbox{P}/\mbox{poly} \) צץ לרוב כשמתחילים לדבר על מעגלים.

בואו נעבור עכשיו לדבר על ההגבלות שמשיתים על מעגלים בוליאניים. כבר רמזתי שמגבילים את גודל המעגל, כלומר את מספר השערים שבו, וזה טבעי לגמרי - אם אתם בונים מעגל חשמלי אמיתי לחישוב פונקציה, תרצו להשתמש בכמה שפחות שערים מכיוון שהם תופסים מקום, צורכים חשמל ומייצרים חום. אבל אני רוצה לדבר גם על הגבלה אחרת - עומק המעגל. עומק המעגל הוא אורך המסלול הארוך ביותר בו - מסלול משערי הכניסה אל שער הפלט. אפשר לחשוב על האורך הזה בתור הזמן שלוקח למעגל לבצע את החישוב שלו, בעוד שעל כמות השערים אפשר לחשוב בתור הזכרון שנדרש לו לצורך החישוב (זה לא מדויק אבל זו אנלוגיה טובה מספיק שתעזור לי בהמשך). במובן הזה אפשר לחשוב על מעגל כאילו הוא מסמלץ חישוב מקבילי: כל השערים במרחק 1 משער הכניסה מבצעים את החישוב שלהם “בו זמנית”, את תוצאות החישוב הם מעבירים לשערים שבמרחק 2 (ואף לשערים מרוחקים יותר), אלו מעבדים את המידע ומעבירים אותו קדימה וכן הלאה. העניין הוא בכך ששער במרחק \( n \) מהכניסה לא תלוי בשום צורה בפלט של שערים אחרים שבמרחק \( n \) מהכניסה, ולכן כל השערים במרחק \( n \) מהכניסה יכולים לבצע את החישוב שלהם בו זמנית.

וכאן מתחיל להתברר לנו שצריך לחזק קצת את המגבלות שלנו אחרת לא נצליח לתאר שום דבר מעניין. נתחיל מכך שכל פונקציה בוליאנית - כל פונקציה - ניתן לחשב עם מעגל שעומקו המביך הוא 2. הסיבה לכך היא שכל פונקציה בוליאנית ניתן לתאר בצורה קנונית: לתאר אותה בתור \( \vee \) אחד גדול על המון \( \wedge \)-ים. מה הרעיון? אם \( f \) היא פונקציה בוליאנית, אפשר לחלק את הקלטים בעולם לשניים - אלו שמחזירים 0 ואלו שמחזירים 1. אז אפשר לתאר את הפונקציה בתור “החזירי אחד אם הקלט שלך הוא \( a \), או אם הוא \( b \), או אם הוא \( c \), או…” כש-\( a,b,c \) וכדומה כולן סדרות ביטים שעבורן \( f \) מקבלת 1. את זה מתארים בתור \( \vee \). כדי לתאר את “הקלט \( x \) שווה ל-\( a \)” צריך בעצם להגיד משהו בסגנון “הביט הראשון של \( x \) שווה לביט הראשון של \( a \), וגם הביט השני של \( x \) שווה לביט השני של \( a \), וגם…” - את זה מתארים בתור \( \wedge \). זה הכל. לצורה הקנונית המתקבלת קוראים DNF.

בתור דוגמה, הנה דרך לתאר את \( \oplus \) כ-DNF. כזכור, זו פונקציה שמקבלת 1 אם ורק אם שני הקלטים (שנסמן כ-\( x_{1},x_{2} \)) שונים זה מזה. כלומר, הקלט הוא \( 01 \) או \( 10 \). הצורה הנורמלית המתאימה היא \( \left(x_{1}\wedge\neg x_{2}\right)\vee\left(\neg x_{1}\wedge x_{2}\right) \).

אם כן, יש לנו כאן מעגל מעומק 2: בשכבה הראשונה יהיו לנו שערי \( \wedge \) עבור כל ההשמות שנותנות 1, ובשכבה השניה יהיה לנו שער בודד, שער הפלט, עם \( \vee \) עליו. אז למה הסתבכנו כל כך עד כה? הסיבה היא שהמעגל שלנו אולי לא עמוק, אבל הוא מאוד לא יעיל: עבור רוב הפונקציות, מספר שערי ה-\( \wedge \) שנזדקק להם הוא אקספוננציאלי ב-\( n \), כי יהיה מספר אקספוננציאלי ב-\( n \) של קלטים עליהם \( f \) מחזירה 1. בעצם אמרנו שאם יש לנו המון, המון מעבדים, אז אפשר לחשב כל פונקציה מהר. טוב ויפה, אבל אז המודל שלנו לא ריאליסטי; אנחנו רוצים לבדוק מה מעגלים יכולים לבצע גם בזמן יעיל וגם בזכרון יעיל. לכן מראש בכל הדיון שלנו מגבילים את גודל המעגלים להיות פולינומי, ואז כל הבניה שהצגנו לא שווה כלום, ועבור רוב הפונקציות לא נצליח למצוא מעגל מעומק 2, או אפילו מעומק קבוע.

חישוב מקבילי הוא מעניין רק אם הוא משיג שיפורים משמעותיים בזמן הריצה אל מול חישובים לא מקביליים. אם חישוב לא מקבילי יעיל הוא כזה שזמן הריצה שלו הוא פולינומי, אין טעם לקרוא גם לחישוב מקבילי “יעיל” אם זמן הריצה שלו פולינומי; לעומת זאת, זמן ריצה לוגריתמי זה כבר משהו מרשים. גם לוגריתמי-בריבוע זה עדיין טוב, ובאופן כללי זמן ריצה פולי-לוגריתמי (שהוא פולינום, אבל לא ב-\( n \) אלא ב-\( \log n \) - למשל \( \log^{7}n+3\log^{3}n+7 \) הוא דוגמה לפולינום ב-\( \log n \)) הוא זמן ריצה מקבילי טוב. כמובן, ככל שהחזקה של הלוגריתם גבוהה יותר כך החישוב טוב פחות. זה מוביל אותנו להגדרה הבאה: \( \mbox{AC}^{k} \) הוא אוסף כל הפונקציות שניתן לחשב על ידי מעגל בוליאני (בעצם משפחת מעגלים בוליאניים אבל כבר הבנתם את העיקרון) מגודל פולינומי ב-\( n \) ובעומק שהוא \( O\left(\log^{k}n\right) \). כך למשל \( \mbox{AC}^{0} \) הוא הפונקציות שניתן לחשב על ידי מעגל מגודל פולינומי ועומק קבוע; \( \mbox{AC}^{1} \) הוא הפונקציות שניתן לחשב על ידי מעגל פולינומי מעומק לוגריתמי, וכן הלאה. ב-\( \mbox{AC} \) מסמנים את איחוד כל המחלקות הללו.

גם המחלקה \( \mbox{AC} \) היא לא ריאליסטית עד הסוף, מהטעם הפשוט שלשערי ה-\( \wedge \) ו-\( \vee \)יכולים להיכנס כמה קלטים שרק נרצה. בפועל, לחשב \( \wedge \) של 100 קלטים לוקח יותר זמן מלחשב \( \wedge \) של 2 כאלו. לכן מוגדרת מחלקה מקבילה ל-\( \mbox{AC} \), שנקראת \( \mbox{NC} \). \( \mbox{NC}^{k} \) זהה ל-\( \mbox{AC}^{k} \) בהגדרתו פרט לכך שדורשים שלשערי \( \wedge,\vee \) ייכנסו ביטים משני שערים בדיוק (מה שמכונה Fan-in 2). זו לא מגבלה עד כדי כך חמורה: אפשר לסמלץ שער \( \vee \) שנכנסים אליו המוני קלטים באמצעות סדרה של שערי \( \vee \) שפועלים הדרגתית על זוגות מתוך הקלטים הללו. דבר כזה יוצר ניפוח לוגריתמי בעומק של המעגל (כי כל צעד קבוע מוחלף על ידי סדרת צעדים שגודלה עשוי להיות פולינומי) ומכאן מתקבלת סדרת ההכלות הבאה: \( \mbox{NC}^{0}\subseteq\mbox{AC}^{0}\subseteq\mbox{NC}^{1}\subseteq\mbox{AC}^{1}\subseteq\mbox{NC}^{2}\subseteq\dots \). כדי לראות שכן יש הבדל כלשהו שימו לב ש-\( \mbox{NC}^{0} \) מכיל רק פונקציות שתלויות במספר קבוע (שאינו תלוי ב-\( n \)) של ביטים מהקלט שלהן, בעוד שב-\( \mbox{AC}^{0} \) זה לא כך.

המחלקה \( \mbox{AC}^{0} \) מעניינת במיוחד מכיוון שהיא שדה הקרב שבו תורת הסיבוכיות נחלה את אחד מנצחונותיה הגדולים עד כה - הוכחה לכך שהפונקציה \( \oplus \) (כשהיא מוגדרת על \( n \) משתנים ולא רק שניים - אפשר לחשוב עליה כאילו היא מבצעת חיבור מודולו 2) לא שייכת ל-\( \mbox{AC}^{0} \) (ולכן גם פונקציות מסובכות יותר רבות אחרות לא - כל מה שאפשר היה להשתמש בו כדי לחשב גם את \( \oplus \)). זו דוגמה לסוג החסמים התחתונים שאחריהם תורת הסיבוכיות מחפשת - הוכחה שיש בעיות קונקרטיות שהן קשות עד כדי כך שפשוט לא ניתן לפתור אותן עם מעגל בוליאני מעומק קבוע. לרוע המזל, זה פחות או יותר כל מה שאפשר לומר על \( \mbox{AC} \) ו-\( \mbox{NC} \) מבחינת חסמים תחתונים קונקרטיים, לפחות כיום. ישנן עוד מספר תוצאות מעניינות על מעגלים, אך הן מתייחסות למקרים עוד יותר ספציפיים שלא מעגלים שלא אכנס אליהן כרגע. הקרב עודנו בעיצומו, גם בימים אלו, אבל לתחושתי המאוד בלתי מלומדת, עיקר התקווה כיום הוא במציאת מודל חדש שיוכל להתמודד עם הבעיות ה”גדולות”, ופחות בכך שמעגלים - מעניינים וחשובים בפני עצמם כמו שהם - יהיו מה שיוביל להתמודדות הזו.

בפוסט הבא נתאר מהן תוכניות מתפצלות ונחזור, הפעם באופן יותר פורמלי ומדויק, על מהו משפט ברינגטון.