שאלות ותשובות - מקבץ מס’ 2

אני ממשיך את המסורת שהתחלתי כאן - מענה לשאילתות חיפוש שהביאו אנשים אל הבלוג הזה למרות שהתשובה אליהן לא ממש נמצאת בדף שאליו הגיעו.

1) “בעיה בלתי פתירה מטמטיקה” - יש שני סוגים עקרוניים לבעיות “בלתי פתירות” שאני חושב עליהם - אחד הוא בעיות חישוביות שלא קיים אלגוריתם שפותר - למשל, האם למשוואה דיופנטית כלשהי יש פתרון. השני הוא בעיות שאין להן תשובה חיובית או שלילית - למשל, השערת הרצף, שאותה לא ניתן להוכיח או להפריך מהאקסיומות הסטנדרטיות של תורת הקבוצות. אני עצמי תוהה אם אלו הסוגים היחידים של בעיות בלתי פתירות שניתן לדבר עליהן.

2) “מה זה חוק החילוף” - למשל, הטענה ש-1+3=3+1, כלומר שאם מחליפים את האיבר הימני בשמאלי בביצוע פעולה מסויימת (בדרך כלל כפל או חיבור), תוצאת הפעולה לא משתנה. חשוב לשים לב שזה לא תמיד מתקיים, למשל עבור חיסור: 5-3 שונה מ-3-5. סטודנטים למתמטיקה בדרך כלל נתקלים בשם הלועזי של התכונה הזו - קומוטטיביות - ומתעסקים עם יצורים רבים שדווקא לא מקיימים אותה (כפל מטריצות, הרכבת תמורות…)

3) “איך יודעים שזאת הסתברות” - השאלה לא הכי ברורה, כמובן, אבל אם נתונה לנו פונקציה שאמורה להיות פונקצית הסתברות (כלומר, לכל תוצאה אפשרית של ה”ניסוי” הבסיסי במרחב ההסתברות שלנו - כמו הטלת קוביה, למשל - מתאימה ערך מספרי כלשהו שהוא ההסתברות שהתוצאה הזו תתקבל) הרי שסכום הערכים שהיא נותנת על כל התוצאות האפשריות אמור להיות 1 (אני מתייחס כאן רק למרחבי הסתברות בדידים - במרחבים רציפים העסק מסובך יותר ודורש דיון נפרד).

4) “נפילת התאומים לפי התורה” - הנושא ראוי לפוסט נפרד (שיגיע) אבל בינתיים, הבהרה קלה - זה בולשיט.

5) “מרחב הילברט הסבר” - מרחב הילברט הוא מושג מתחום מתקדם יחסית (דהיינו, כזה שדורש קורס יסוד אחד או שניים להבנתו) במתמטיקה שנקרא “אנליזה פונקציונלית”. בבסיסו, מרחב הילברט הוא מרחב וקטורי, מושג שדורש הסבר בפני עצמו (לעת עתה אפשר לחשוב על מרחב וקטורי כעל הכללה של המרחב ה-2 והמרחב ה-3-ממדי). על המרחב הוקטורי הזה הוגדר מושג נוסף, של מכפלה פנימית (מושג שניתן לחשוב עליו כהכללה של מושג הזווית). מהמכפלה הפנימית מושרה מושג של נורמה (שהוא הכללה של מושג האורך). מהנורמה מושרית מטריקה (שהיא הכללה של מרחק), מה שהופך את המרחב הוקטורי בפרט למרחב מטרי. במרחבים מטריים קיים מושג של “שלמות”, שפירושו שכל סדרה ש”נראית מתכנסת” (המושג המדוייק הוא “סדרת קושי” - סדרה שהמרחק בין איבריה שואף לאפס) אכן מתכנסת לאיבר מתוך המרחב (דוגמה למרחב לא שלם - הרציונליים, כי יש סדרות של רציונליים שמתכנסות למספר אי רציונלי שאינו חלק מהמרחב).

מרחב הילברט הוא מרחב מכפלה פנימית ששלם ביחס למטריקה שמושרית מהנורמה שלו. השלמות הזו גורמת לכך שהרבה תכונות “נחמדות”, שבמרחבי מכפלה פנימית כלליים לא מתקיימות, כן יתקיימו במרחב ההילברט, ומכיוון שמרחבים רבים ומועילים הם מרחבי הילברט, יש בהם עניין רב. בפרט, מרחבי הילברט צצים כשעוסקים בחקר פונקציות ומשוואות דיפרנציאליות - יצורים מסובכים לכאורה, שיש יתרון רב בכך שניתן להפעיל עליהם שיקולים מאלגברה לינארית - דהיינו, שיקולים שבבסיסם הם הכללה לא מורכבת של רעיונות מהגאומטריות של המישור והמרחב.

הסיבה שבגללה לא שומעים על מרחבי הילברט עד לשלב מאוחר יחסית בלימודים, ולא ישר כשלומדים על מכפלות פנימיות היא שכל עוד מדברים על מרחבי מכפלה פנימית סוף-ממדיים (כלומר, שקיימת קבוצה סופית של איברים כך שניתן לתאר כל איבר במרחב בתור צירוף שלהם), כל מרחב מכפלה פנימית הוא אוטומטית הילברט, אז אין צורך לציין את המושג הזה במפורש; לכן המושג צץ ועולה רק כשמתחילים לדבר על מרחבים אינסוף ממדיים, שהם הנושא שבו עוסקת האנליזה הפונקציונלית.

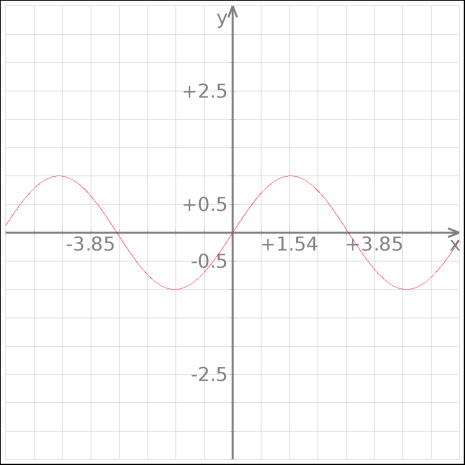
6) “גרף סינוס וקוסינוס” - הנה גרף סינוס:

גרף של קוסינוס הוא אותו הדבר בדיוק, פרט לכך שצריך “להזיז” אותו טיפה שמאלה, כך שראש הגבעה הראשונה מימין לציר y תהיה בדיוק על ציר y.

7) “בלי הגבלת הכלליות באנגלית” - Without loss of generality. הכוונה היא לכך שמניחים הנחה כלשהי בזמן הוכחה שאינה פוגעת בכלליות של ההוכחה - דהיינו, שאינה מצמצמת את ההוכחה למקרה פרטי יותר, שרק בו ההנחה מתקיימת, מכיוון שניתן בצורה פשוטה (לפעמים מגוחכת לגמרי, כמו שינוי סימון) לעבור מהמקרה הכללי למקרה הפרטי (ולכן הוכחה עבור המקרה הפרטי נכונה גם עבור הכללי).

8) “פונקצית אוילר היא כפלית” - ההוכחה לכך אינה מיידית. הוכחה פשוטה אחת מתבססת על כך ש-\( \mathbb{Z^*}_{m\times n}\approx\mathbb{Z^*}_{m}\times\mathbb{Z^*}_{n} \) אם m,n זרים, ושפונקצית אוילר היא בדיוק גודל החבורות הללו. כדי להוכיח את האיזומורפיזם הזה משתמשים במשפט השאריות הסיני.

9) “פיצוח פנקס חד פעמי” - תשכחו מזה. אי אפשר. כמובן, ברגע שהפנקס מפסיק להיות חד פעמי ומשתמשים בו לפחות פעמיים, אפשר; בפרט, אם נתונים שני כתבי סתר שהוצפנו בעזרת אותו פנקס, אז ביצוע XOR עליהם יניב את ה-XOR של הכתבים הגלויים המקוריים. שמעתי שמועות לפיהן אפשר מ-XOR שכזה (ובהינתן שידוע משהו על הסטטיסטיקה של הטקסטים שהוצפנו - למשל, שהם באנגלית) אפשר להפיק הרבה מידע.

10) “למה חשוב לדעת לוח כפל” - כי ידיעה של לוח הכפל מאפשרת לכפול כל מספר שרק רוצים, בהינתן דף ועט. השאלה הרלוונטית יותר היא למה חשוב בכלל לדעת לבצע פעולות חשבון, בעולם שבו קיימים מחשבונים; התשובה היא שלא תמיד יש לך מחשבון זמין ובמקרים רבים מאוד, ביצוע חישוב פשוט בראש הוא מהיר הרבה יותר מאשר מציאת מחשבון והפעלתו. הסבר פחות “תועלתני”, אך אולי יותר “מדעי” הוא שתמיד כדאי לדעת כמה שיותר על המכונות שבהם משתמשים ואיך הן מבצעות את מה שהן מבצעות - בורות, כידוע, איננה תכונה בריאה לדמוקרטיה בפרט ולאנושות בכלל, וכולנו זוכרים מי אמר שהיא כוח.