אז מה זה בעצם חוג?

סדרת הפוסטים שלי על אלגברה מופשטת התחילה עם המון פוסטים על חבורות. עכשיו סיימנו את הנושא הזה, פחות או יותר, ואנחנו עוברים אל הנושא המתבקש הבא: חוגים. אבל מה זה חוג? באופן שבו מלמדים את זה על פי רוב, חוג הוא “חבורה שהוסיפו לה עוד משהו”. זו לא דרך התבוננות רעה; בפרט, היא מאפשרת לקחת הרבה מאוד מהרעיונות שצצו כשהתעסקנו עם חבורות ולהעביר אותם פחות או יותר ללא שינוי מהותי גם אל תורת החוגים. אבל זה לא האופן ההיסטורי שבו מושג החוג התפתח, וזו גם לא התשובה שאני רוצה לתת למישהו שבכלל לא מכיר חבורות ובכל זאת רוצה לדעת מה זה חוג. אז נתחיל מלהסביר מה זה בעצם ורק אחר כך נקשר את זה במפורש לחבורות.

האבטיפוס של חוג הוא המספרים השלמים. במובן מסויים הכל התחיל מהם. מה אפשר לעשות עם מספרים שלמים? אפשר לחבר אותם. אפשר לחסר אותם. אפשר לכפול אותם. אפשר לחלק… רגע, צריך להיות זהירים. אחד לחלק לשתיים זה \( \frac{1}{2} \), שאינו מספר שלם. מה שאפשר לעשות במקרה הזה הוא לחלק עם שארית, אבל זו כבר פעולה קצת מסובכת. הפעולות הבסיסיות שאנחנו דבקים בהן הן שלושת הראשונות: חיבור, חיסור, כפל. גם על חיסור אפשר לוותר במידה מסויימת: \( a-b \) זו דרך אחרת לומר \( a+\left(-b\right) \); כלומר, במקום לחסר את \( b \) מ-\( a \) אנחנו הולכים אל הצד השני של ציר המספרים, פוגשים את הנגדי של \( b \), ומחברים אותו ל-\( a \). לכן הדברים שאנחנו רוצים לדבר עליהם כשאנחנו מדברים על חוג הפכו להיות שלושה: פעולת חיבור, פעולת כפל, וקיום “נגדי” לפעולת חיבור. כדי להגדיר נגדי בצורה טובה אנחנו צריכים גם לדבר במפורש על 0: הנגדי של \( a \) הוא המספר שכשמחברים אותו ל-\( a \) מקבלים 0. גם זה משהו שקיים, כמובן, במספרים השלמים.

אז הנה המרכיבים של המספרים השלמים שאנחנו רוצים לקחת איתנו הלאה אל ההכללה: פעולת חיבור, פעולת כפל, קיום איבר אדיש לחיבור (0) וקיום איבר נגדי לחיבור (מינוס). עוד דבר אחד שנותר לנו לדרוש הוא שפעולות החיבור והכפל “יתנהגו יפה”. בואו ניזכר מה התכונות של הפעולות הללו שנלמדות בבית הספר היסודי:

1. חוק הקיבוץ: \( a+\left(b+c\right)=\left(a+b\right)+c \)
2. חוק החילוף: \( a+b=b+a \)
3. חוק הפילוג: \( a\cdot\left(b+c\right)=a\cdot b+a\cdot c \)

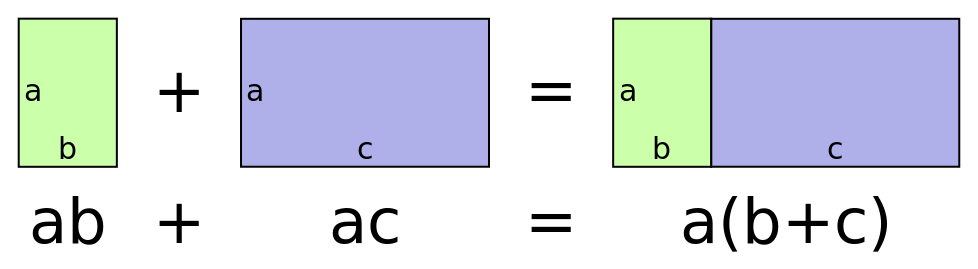
אני רגיל לקרוא לחוקים הללו בשמות הלועזיים שלהם: אסוציאטיביות לחוק הקיבוץ, קומוטטיביות לחוק החילוף, דיסטריביוטיביות לחוק הפילוג. המשמעות של אסוציאטיביות היא שאם יש לנו הפעלה של שתיים או יותר פעולות חיבור ברצף, זה לא משנה את מי מהן נפעיל קודם; המשמעות של קומוטטיביות היא שאם יש לנו פעולת חיבור, זה לא משנה מה הסדר בין המחוברים - מי ימני ומי שמאלי. את שני אלו הסברתי גם בפוסטים על חבורות. דיסטריביוטיביות היא משהו חדש, כי היא מתארת לנו איך כפל משחק יחד עם חיבור. אינטואיטיבית, היא אומרת שאם אני מפרק איבר לסכום של כמה חלקים, אז אני יכול לכפול כל אחד מהחלקים הללו בנפרד ב-\( a \), ואחר כך לחבר אותם בחזרה ביחד ולקבל את המכפלה של האיבר המקורי ב-\( a \). התכונה הזו מועילה מאוד, ונראה איך משתמשים בה שוב ושוב. הנה ויזואלציה פשוטה שלה כשמדובר על חיבור וכפל של מספרים ממשיים:

הרעיון כאן הוא שאם יש לנו מלבן שאורך אחד מצלעותיו הוא \( a \) ואורך הצלע השניה שלו ניתן לפירוק לשני אורכים שונים, \( b+c \), אז אפשר לטפל בכל מלבן בנפרד, לחשב את השטח שלו, ואז לחבר את שטחי שני המלבנים שקיבלנו. שימו לב שבדוגמא הזו החיבור בעצם מתאר שתי סיטואציות שונות: החיבור ה”מקורי” הוא של אורכי קטעים ואילו החיבור שלאחר מכן הוא של שטחי מלבנים (בשני המקרים גם האורך וגם השטח מיוצגים על ידי מספרים ממשיים ולכן זה “עובד”). בדרך כלל אצלנו לא תהיה הבדלה רעיונית כזו.

האסוציאטיביות והקומוטטיביות שתיארתי קודם היו עבור פעולת החיבור; אבל מה עם פעולת הכפל? ובכן, כאן העניינים מסתבכים. עבור פעולת הכפל על פי רוב אנחנו דורשים פחות דברים מאשר עבור פעולת החיבור. למה? מהטעם הפשוט שהאובייקטים המתמטיים הקונקרטיים שמהמחקר שלהם התפתחה תורת החוגים לאו דווקא קיימו אותן. אבל אילו תכונות כן דורשים? על פי רוב אלו שתי התכונות הבאות:

1. חוק הקיבוץ: \( a\cdot\left(b\cdot c\right)=\left(a\cdot b\right)\cdot c \)
2. קיום איבר אדיש לכפל: קיים איבר שמסומן בתור \( 1 \) כך ש-\( 1\cdot a=a\cdot1=a \) לכל \( a \) בחוג.

אפילו שתי הדרישות הללו לא חקוקות באבן: אם תגגלו תמצאו בקלות שקיים מושג של “חוג לא אסוציאטיבי” וגם תגלו שבהחלט מדברים לפעמים על חוגים בלי איבר יחידה כפלי (באנגלית חוג נקרא Ring ולפעמים משתמשים בכתיב המזעזע Rng כדי לתאר חוג ללא יחידה). על אסוציאטיביות בדרך כלל לא נהוג לוותר והמבנים הלא אסוציאטיביים שכן מתעסקים בהם (למשל, אלגבראות לי) מגיעים עם מבנה קצת יותר עשיר מאשר “רק” מבנה של חוג. על יחידה כן אפשר לוותר, אבל אני חושב שיהיה לי יותר נוח להניח אוטומטית שבכל החוגים שלי יש יחידה אלא אם נאמר אחרת, ובמקרה הזה לדבר על “חוג בלי יחידה” (או סתם להתעלם מהמחסור הזה אם אני לא זקוק לאיבר היחידה הזה).

מה בוודאי אין? קומוטטיביות של כפל לא בהכרח מתקיימת. למעשה, אפשר לחלק באופן גס את האלגברה המופשטת לשני “סוגים” - אלגברה קומוטטיבית שמתעסקת בחוגים קומוטטיביים, ואלגברה לא קומוטטיבית שמתעסקת בחוגים לא קומוטטיביים. ברצינות, תבדקו, השמות הללו קיימים וזו המשמעות שלהם. עד כדי כך ההפרדה הזו היא קריטית. כדי לתת אינטואיציה גסה מאוד, לפני שנגיע לדוגמאות בהמשך - תחשבו על אלגברה קומוטטיבית כתחום שמתעסק בדברים שהם “כמו מספרים”, ועל אלגברה לא קומוטטיבית כתחום שמתעסק בדברים שהם “כמו מטריצות” (גישת ה”כמו מספרים” נשברת בקלות עם הקווטרניונים, שהם לא קומוטטיביים ולמעשה הכי נכון לתאר בעזרת מטריצות, אבל נעזוב את זה כרגע).

עוד דבר שבדרך כלל אין הוא הופכי כפלי. כלומר, בהינתן \( a \) בחוג, על פי רוב לא יהיה \( b \) כך ש-\( ab=1 \). לא קשה לראות שאם \( a=0 \) אז אף פעם לא יכול להיות כזה, אבל אפשר לדבר על מקרים שבהם יש הופכי לכל מי ששונה מאפס. חוג שבו יש הופכי לכל מי ששונה מאפס נקרא חוג עם חילוק (הקווטרניונים הם דוגמא), וחוג עם חילוק שהוא גם קומוטטיבי נקרא שדה. שדות הם מקרים פרטיים של חוגים, אבל מקרים מאוד, מאוד מעניינים בפני עצמם, ויש תחום שלם שמתעסק בהם - תורת השדות, שאליו מגיעים בדרך כלל אחרי היכרות כלשהי עם תורת החוגים (למעשה, שדות צצים כבר בלימודי אלגברה לינארית, אבל שם הם על תקן הופעת אורח שכזו ולא האובייקט האמיתי שחוקרים).

יש כמובן עוד סיווגים שונים ומשונים שאפשר להשית על חוגים, אבל רובם יהיו חסרי משמעות עבורנו בשלב הזה. למשל, יש חשיבות גדולה לחוגים שמהווים מה שנקרא תחום ראשי, אבל תחום ראשי מוגדר בתור חוג שהוא “תחום שלמות שבו כל אידאל נוצר בידי איבר יחיד” וזה משתמש בהמון טרמינולוגיה ספציפית לתורת החוגים שטרם הגענו אליה, אז בואו נעצור כאן את הדיון על סוגים שונים ומשונים של חוגים, ונדבר קצת על האובייקטים המתמטיים העיקריים שבהם מתעסקים בתורת החוגים. חשוב לי לחדד שתורת החוגים התפתחה מתוך האובייקטים הללו, לא ההפך: זה לא שהמתמטיקאים המציאו את המושג של חבורה, אמרו “וואו איזה נחמד בואו נוסיף עוד פעולה לתמונה ונשחק איתה” ואז התחילו לחפש דברים מתמטיים שיתאימו למבנה שהם מתארים; תורת החוגים התחילה מתוצאות קונקרטיות על אובייקטים קונקרטיים שמתמטיקאים זיהו בהם את המשותף והכלילו את התוצאות עליהם.

ובכן, הדוגמא הפשוטה ביותר לחוג היא כאמור השלמים, \( \mathbb{Z} \). זו דוגמא לחוג קומוטטיבי אבל כמובן שללא חילוק - רק ל-\( 1 \) ול-\( -1 \) קיים הופכי. מה שכן יש בשלמים הוא חילוק עם שארית; זה הופך את השלמים למשהו שנקרא חוג אוקלידי אבל על זה נדבר בהמשך. מה שנחמד הוא שדבר דומה קיים עבור פולינומים: אם \( \mathbb{F} \) הוא שדה כלשהו, אז אוסף הפולינומים עם מקדמים מעל אותו שדה, \( \mathbb{F}\left[x\right] \), הוא חוג קומוטטיבי, וגם בו מתקיימת תכונת החילוק עם שארית, כפי שכל מי שלמד אלגברה לינארית בוודאי כבר ראה פעם. זה הופך את השלמים ואת הפולינומים לחוגים עם אופי די דומה, אם כי בצורה מעניינת דווקא הפולינומים מרגישים לפעמים פשוטים יותר (למשל, בעיית הפירוק לגורמים של פולינום היא יותר קלה מפירוק לגורמים של מספר שלם).

את הסיפור הבסיסי הזה אפשר להכליל בכמה כיוונים. ראשית, השלמים ניתנים להרחבה לאובייקט גדול יותר, \( \mathbb{Q} \), שבו לכל איבר פרט ל-0 יש הופכי; הבניה של \( \mathbb{Q} \) מ-\( \mathbb{Z} \) היא דוגמא לבניה סטנדרטית של שדה שברים של חוג. \( \mathbb{Q} \) כבר מעביר אותנו לתחום של תורת השדות, וכך גם ההרחבות שלו \( \mathbb{R} \) ו-\( \mathbb{C} \) (אם כי במובן מסויים \( \mathbb{R} \) ו-\( \mathbb{C} \) הם “גדולים מדי” עבור תורת השדות הבסיסית - הם מה שנקרא הרחבה טרנסנדנטית של \( \mathbb{Q} \), אבל גם על זה נדבר בפעם אחרת).

דרך אחרת להרחיב את \( \mathbb{Z} \) היא על ידי הוספה של “קצת” איברים שהם מצד אחד לא מספרים רציונליים, ומצד שני מתנהגים באופן דומה למספרים השלמים. הנה הדוגמא הקלאסית: פרמה העלה את השאלה עבור אילו מספרים ראשוניים \( p \) קיים פתרון למשוואה בשלמים \( x^{2}+y^{2}=p \), כלומר אילו ראשונים אפשר להציג בתור סכום של שני ריבועים שלמים. התשובה היא שקיים פתרון כזה אם ורק אם \( p \) הוא 2 או משאיר שארית 1 בחלוקה ב-4, אבל איך מגיעים לכזה פתרון? ובכן, אבחנה יפהפיה היא שאפשר לחשוב על הביטוי \( x^{2}+y^{2} \) גם בתור מכפלה אם אנחנו חופרים עמוק מספיק מתחת לשלמים: \( x^{2}+y^{2}=\left(x+iy\right)\left(x-iy\right) \). שני המספרים \( x+iy \) ו-\( x-iy \) הם לא מספרים שלמים, אבל הם דומים למספרים שלמים. אם לחדד - הקבוצה \( \mathbb{Z}\left[i\right]=\left\{ a+bi\ |\ a,b\in\mathbb{Z}\right\} \) היא חוג שהתכונות שלו דומות מאוד לתכונות של \( \mathbb{Z} \) (למשל, גם זה חוג אוקלידי). מבלי להיכנס כרגע לפרטים המלאים, חקירה של תכונות החוג הזה מצביעה על כך שאם \( p \) הוא ראשוני שלם, אז אם \( p\equiv_{4}3 \) הוא יישאר ראשוני גם ב-\( \mathbb{Z}\left[i\right] \) אבל אם \( p\equiv_{4}1 \) אז הוא יהפוך להיות פריק בתוך \( \mathbb{Z}\left[i\right] \), והפירוק לגורמים שלו בהכרח יהיה מהצורה של מספר והצמוד המרוכב שלו, כלומר בדיוק הסיטואציה \( \left(x+iy\right)\left(x-iy\right) \). זו הוכחה מעניינת כי היא מתבססת על ההיכרות שלנו עם המבנה של החוג \( \mathbb{Z}\left[i\right] \) ולא על טריקים ייעודיים (אפשר לראות הוכחה עם טריקים ייעודיים כאן). החוג \( \mathbb{Z}\left[i\right] \) נקרא השלמים הגאוסיים והמחקר שלו היה אחד מהחלוצים של תורת החוגים.

יש עוד דרכים “להרחיב” את \( \mathbb{Z} \) על ידי הוספת מספרים לא שלמים מתאימים על מנת לקבל חוגים חדשים. למשל, לכל \( D \) שלם, החוג \( \mathbb{Z}\left[\sqrt{D}\right]=\left\{ a+b\sqrt{D}\ |\ a,b\in\mathbb{Z}\right\} \) הוא חוג מעניין בפני עצמו (עבור \( D=-1 \) מקבלים את השלמים הגאוסיים). התכונות של החוגים הללו תלויות מאוד ב-\( D \); למשל, כמעט אף פעם לא נקבל חוג אוקלידי נחמד כמו ב-\( \mathbb{Z}\left[i\right] \). ככל הנראה הדרך הנכונה לראות את החוגים הללו היא בהקשר שמכיר גם את תורת השדות; בתורת השדות אפשר לדבר על הרחבות של \( \mathbb{Q} \) על ידי הוספת מספרים לא רציונליים אליו, והתוצאה היא שדה גדול יותר; בשדה כזה אפשר לאתר את ה”שלמים” שלו, בדומה לאופן שבו \( \mathbb{Z} \) הם השלמים של הרציונליים. לשלמים מוכללים כאלו קוראים שלמים אלגבריים והתחום שעוסק בהם נקרא תורת המספרים האלגברית. כבר כתבתי בעבר סדרת פוסטים שמהווה מבוא לתחום הזה.

את חוג הפולינומים מעל שדה אפשר להרחיב בצורה קצת שונה: להתעסק בפולינומים במספר משתנים. במקרה הזה שוב עשויים להתקבל חוגים מורכבים מאוד, הרבה יותר מאשר במקרה של משתנה יחיד. פולינומים במספר משתנים מעניינים, למשל, בגלל היכולת שלהם לתאר אובייקטים גאומטריים: כך למשל מעגל הוא אוסף הערכים שמאפסים את הפולינום \( x^{2}+y^{2}-R^{2} \) עם המשתנים \( x,y \) (\( R \), הרדיוס, הוא פרמטר של הפולינום) וקו ישר הוא אוסף הערכים שמאפסים את \( ax+by-c \) וכן הלאה. הקשר ההדוק הזה שבין אובייקטים גאומטריים ובין המשוואות שמתארות אותם היא נקודת הפתיחה של תחום הגאומטריה האלגברית, שגם היא אחד מהתחומים החשובים במתמטיקה כיום.

שני התחומים הללו - תורת המספרים האלגברית והגאומטריה האלגברית - היו הבסיס שממנו צמחה האלגברה הקומוטטיבית, ובדרך כלל אכן לומדים קורס בסיסי באלגברה קומוטטיבית בתור הכנה לשניהם. אין לי ממש יכולת לכתוב משהו מעבר לדברים טריוויאליים לחלוטין על שני התחומים הללו בפוסטים שאני מתכנן, אבל אני מקווה לגעת קצת בתוכן של מה שנקרא “אלגברה קומוטטיבית” (ובפועל אפשר לחשוב עליו בתור המשך לחומר הבסיסי של חוגים).

אלו היו דוגמאות לחוגים קומוטטיביים. בצד הלא קומוטטיבי, הדוגמא הראשונה, מייסדת הז’אנר, היא הקווטרניונים של המילטון, וכל מני הכללות שלהם (אוקטניונים, ביקווטרניונים ושאר מריעין בישין). פרט לכך, הדוגמאות הבולטות ביותר לחוגים לא קומוטטיביים הם חוגים של מטריצות. מטריצות היו גם דוגמא טובה לחבורות לא אבליות, אבל יש להן מבנה נוסף, של פעולת חיבור, ולכן הקשר יותר מתאים לדבר עליהן הוא ההקשר של חוגים (ליתר דיוק, ההקשר המתאים לדבר עליהן הוא ההקשר שבו מטריצות הן גם איברים של מרחב וקטורי; משתמשים בשם אלגברה כדי לתאר מרחב וקטורי שהוא גם חוג).

יש עוד דוגמאות לחוגים משלל סוגים שלא אמרתי עליהם כלום (למשל, חוגים של פונקציות), אבל אני מניח שהרעיון ברור. המושג של חוג הוא מושג שימושי בצורה יוצאת דופן - אחד מהנפוצים ביותר במתמטיקה. זה הופך את תורת החוגים לעמוד השדרה של כל האלגברה המופשטת - ומן הסתם לא אוכל לומר עליה עד כדי כך הרבה בסדרת הפוסטים שאני מתכנן. אבל נתחיל מהמושגים הפשוטים ונראה לאן נגיע.