למה מינוס כפול מינוס זה פלוס?
מבוא
ביקשו ממני להסביר דבר פשוט לכאורה שכולם לומדים בבית הספר היסודי: שמינוס כפול מינוס הוא פלוס. אם לדבר קונקרטית, ש-\( \left(-3\right)\times\left(-5\right)=15 \). למה? למה זה נכון? לשאלה הזו יש שתי תשובות מיידיות. הראשונה היא שזה נובע מייד מהתכונות הבסיסיות של כפל ומהאופן שבו מוגדרים המספרים השליליים. זו התשובה הנכונה מבחינה מתמטית, והיא כמובן תשובה איומה ונוראה, כי היא לא באמת נותנת לנו אינטואיציה למה שהדבר הזה יהיה נכון. במושגים כל כך בסיסיים אנחנו מצפים שהמתמטיקה תשרת את האינטואיציה ולא ההפך. אם כן, מה התשובה האינטואיטיבית ביותר? ללא ספק - שלילה כפולה. כולנו יודעים ששלילה כפולה מבטלת את עצמה. לומר “אין זה נכון שמספרים שליליים הם לא מגניבים” זו דרך מסובכת לומר “מספרים שליליים הם מגניבים”. לומר “עמדתך המנומקת בקפידה לגבי המספרים השליליים היא לא לא נכונה” זו דרך גרועה להגיד “עמדתך המנומקת בקפידה לגבי המספרים השליליים היא נכונה”. אם כן, למה גם התשובה הזו לא בהכרח טובה?
ראשית, כי יש בדיחה מפורסמת על בלשן שהיה נוכח בהרצאה של בלשן עמית. הלה הרצה על כך שבכל השפות הידועות שלילה של דבר חיובי היא שלילה (“מינוס כפול פלוס הוא מינוס”) ושלילה של שלילה היא חיוב (“מינוס כפול מינוס הוא פלוס”) אבל חיוב של חיוב הוא לא שלילה (“פלוס כפול פלוס שווה פלוס”). לזה הבלשן שבקהל הגיב ב”כן, בטח”.
כלומר, האנלוגיה לשפה היא לא רעה, אבל צריך להיזהר איתה, היא גם לא מוחלטת.
פרט לכך, אם שלילה של שלילה היא חיוב, למה חיבור של שני מספרים שליליים יוצא שלילי, כלומר \( \left(-3\right)+\left(-5\right)=-8 \)? לאינטואיציה שלי קצת קשה להסתדר עם זה. אז בואו ניתן כמה הסברים אפשריים. אין פה הסבר “נכון”; את ההסבר ה”נכון” אני אציג בסוף. ההסברים הללו יותר טובים מסתם הסבר נכון - אני חושב שהם מסייעים לאינטואיציה, שהיא הדבר החשוב פה.
על בנקים וכדורגל
בואו נתחיל מלדבר על משהו קצת יותר פשוט מאשר כפל: למה לחסר מספר שלילי זה כמו לחבר את המספר החיובי המתאים? כאן הכי טוב ללכת לדוגמאות קונקרטיות. קודם כל אל הדוגמא שתמיד משתמשים בה - כסף. נניח שיש לנו חשבון בנק. הסכום בו מתאר את כמות הכסף שעומדת לרשותנו. אם הסכום שבבנק הוא 1,000 זה אומר שיש לנו 1,000 ש”ח - הבנק חייב לנו 1,000 ש”ח. אם יש לנו בבנק \( -1,000 \) ש”ח זה אומר שאנחנו חייבים לבנק 1,000 ש”ח. עכשיו, לחבר מספר כלשהו לחשבון הבנק שלנו פירושו להגדיל את כמות הכסף שעומדת לרשותנו במספר הזה. תחשבו על מספר חיובי כמייצג רווח ועל מספר שלילי כמייצג הפסד. אם אני מוסיף 200 ש”ח לחשבון זה אומר שהרווחתי מהיכן שהוא 200 ש”ח והם מתווספים לסכום הכולל שלי. אם הסכום היה 1,000, אז אחר כך יהיו לי 1,200 ש”ח. לעומת זאת, אם אני מוסיף \( -200 \) ש”ח זה אומר שהפסדתי 200 ש”ח - שילמתי למישהו על משהו - ועכשיו ההפסד הזה מתווסף לי לחשבון ואני נותר עם 800 ש”ח לזכותי בלבד.
לעומת זאת, לחסר מספר כלשהו פירושו להקטין את כמות הכסף שעומדת לרשותי בהתאם למספר שאני מחסר. אם אני מחסר 200 ש”ח, זה אומר שאני “מוחק” מהחשבון שלי רווח של 200 ש”ח. זה בדיוק כמו “לחבר \( -200 \) ש”ח”, ולא במקרה; בעצם, הרעיון האינטואיטיבי שמאחורי מספר שלילי הוא שלחבר עם מספר שלילי הוא בעל אותו אפקט כמו לחסר את המספר החיובי המתאים. עכשיו, אם אני מחסר מהחשבון של \( -200 \) ש”ח זה אומר שאני “מוחק” מהחשבון שלי הפסד של 200 ש”ח. אם ההפסד נמחק, זה מתורגם לרווח - אני מגדיל את החשבון שלי ב-200 ש”ח.
הנה דוגמא אחרת עם רעיון דומה - כדורגל. בכדורגל התוצאה נספרת תמיד במספרים טבעיים אי-שליליים, אבל תחשבו רגע על ההפרש בין מספר השערים של הקבוצה שלנו והקבוצה היריבה. כאשר ההפרש חיובי, אנחנו מובילים, וכאשר ההפרש שלילי אנחנו בפיגור. עכשיו, אפשר לחשוב על שחקן שלנו שמבקיע לשער היריב כאילו הוא מחבר למאזן שלנו עוד נקודה חיובית אחת - ההפרש גדל לטובתנו. מצד שני, אם הוא מבקיע בטעות גול עצמי אפשר לחשוב על כך כאילו הוא חיבר למאזן שלנו נקודה שלילית אחת. לעומת זאת, כאשר שחקן של היריב מבקיע לשער שלנו המאזן שלנו קטן ב-1 ואילו כשהוא מבקיע לשער שלו בטעות המאזן שלנו גדל ב-1. אפשר לחשוב על זה כך: הבקעה לשער הקבוצה היריבה שווה תמיד \( 1 \) ואילו הבקעה לשער של עצמך שווה \( -1 \). כאשר הקבוצה שלנו מבקיעה (לא משנה לאיזה שער), אנחנו מחברים את הערך של השער למאזן שלנו, ואילו כאשר הקבוצה היריבה מבקיעה אנחנו מחסרים את הערך של השער מהמאזן שלנו. כך יוצא שהבקעה של שחקן יריב לשער של עצמו היא “לחסר \( -1 \) מהמאזן שלנו”, כלומר להוסיף 1.
בדוגמאות הללו מאוד בולטת העובדה שחיבור של מספר שלילי זה כמו חיסור של מספר חיובי. אם שחקן שלנו מבקיע גול עצמי (חיבור של מספר שלילי) האפקט הוא זהה לזה שבו שחקן יריב מבקיע לשער שלנו (חיסור של מספר חיובי). זה לא מקרה; זו בעצם המהות של מספרים שליליים, שחיבור של מספר שלילי יהיה שקול לחיסור, וזה גם מה שמכריח את החיסור של מספר שלילי להיות זהה לחיבור.
הנה עוד דרך יפה לחשוב על זה שמערבת בנקים ורווחים, אבל גם את ציר הזמן. נניח שבכל חודש נכנסת לי משכורת של 1,000 ש”ח לחשבון. אני יכול לשאול את עצמי - בהשוואה למצב החשבון כרגע, מה יהיה מצב החשבון עוד שלושה חודשים אם כל מה שישתנה הוא המשכורת שנכנסת? התשובה היא שיהיו לי עוד 3,000 ש”ח בחשבון - 3 פעמים 1,000 ש”ח. אבל הנה שאלה אחרת - נניח שאני שואל את עצמי מה היה המצב לפני שלושה חודשים ביחס למצב היום: במקרה הזה אני צריך להחסיר 3,000 ש”ח מהמצב היום. כלומר, לכפל במספר שלילי יש משמעות של “חזרה אחורה בזמן”. ועכשיו בואו נעשה את אותו הדבר במקום עם משכורת שנכנסת להוצאה חודשית קבועה, נאמר שכר דירה של 10,000 ש”ח: אם אני מסתכל שלושה חודשים קדימה צפוי לי הפסד של -30,000 ש”ח בגלל שכר הדירה, אבל אם אחזור בזמן שלושה חודשים אחורה אראה שהייתי עשיר ב-30,000 ש”ח יותר שעדיין לא הוצאו על שכר הדירה. הנה איך כפל במספר שלילי (“מספר חודשים אחורה”) של ערך שלילי (“תשלום שכר דירה”) הופך למשהו חיובי.
חזרה אל הכפל
עכשיו בואו נעבור לדבר על כפל. מה זה כפל? כפל של שני מספרים טבעיים הוא “סימון מקוצר לחיבור”. כלומר, כשאני כותב \( 3\times5 \), מה שאני קורא בקול בתור “שלוש פעמים חמש”, אני מתכוון לדבר הבא: \( 5+5+5 \). בגישה הזו אין שום דבר מוזר בביטוי כמו \( 3\times\left(-5\right) \), “שלוש פעמים מינוס חמש”: זה פשוט הביטוי \( -5+\left(-5\right)+\left(-5\right) \). אבל מה על הביטוי ה”הפוך”, \( \left(-3\right)\times5 \), “מינוס שלוש פעמים חמש”? מה המשמעות שלו?
אנחנו רגילים לחשוב על כפל בתור פעולה שבה הסדר לא משנה - שלוש כפול חמש וחמש כפול שלוש נותנים את אותו הדבר. זה מה שנקרא “חוק החילוף”. אם אנחנו מקבלים את האינטואיציה לפיה חוק החילוף צריך להתקיים פה, אז ברור לנו ש”מינוס שלוש פעמים חמש” צריך לצאת כמו “חמש פעמים מינוס שלוש”, כלומר הוא צריך לצאת גם \( -15 \), אבל מה המשמעות של הפעולה עצמה של כפל במספר שלילי?
כדי לראות איך אני רואה את זה, בואו נכתוב שניה את “שלוש פעמים חמש” בצורה קצת יותר מסורבלת: \( 0+5+5+5 \). האפס בהתחלה הוא “אדיש”, כשמחברים אותו הוא לא משנה את הסכום. למה הוא בכלל שם? ובכן, אני חושב כמו מתכנת: כשמתכנת מגדיר משתנה הוא לרוב מאתחל אותו לאיזה ערך “נייטרלי” כמו 0. אז תחשבו על פעולת החיבור כאילו אתחלתי משתנה להחזיק 0 ואז אני מוסיף למשתנה הזה את 5 בדיוק 3 פעמים ורואה מה יצא. עכשיו, לכפול במספר חיובי מתורגם ל”לבצע חיבור כך-וכך פעמים”. אז אני חושב על “לכפול במספר שלילי” בתור “לבצע חיסור כך וכך פעמים”, כלומר “מינוס שלוש פעמים חמש” יתורגם אצלי ל-\( 0-5-5-5 \) שהוא כמובן \( -15 \). בלי האפס בהתחלה הביטוי הזה נראה לי קצת מוזר, כי ה”מינוס” הראשון, השמאלי ביותר, לא נראה כאילו הוא מתאר פעולה בין שני מספרים.
זה היה “מינוס שלוש פעמים חמש”. מה יהיה “מינוס שלוש פעמים מינוס חמש”? זה יהיה לחסר את מינוס 5 שלוש פעמים. כלומר, זה יהיה \( 0-\left(-5\right)-\left(-5\right)-\left(-5\right) \). אם כבר הסכמתם שחיסור של מספר שלילי הוא חיבור, אז קיבלנו ש”מינוס שלוש פעמים מינוס חמש” הוא \( 5+5+5=15 \).
יש עוד דרך לחשוב על כפל במספר שלילי. במקום לומר ש”מינוס שלוש פעמים חמש” זה לחסר את חמש שלוש פעמים, אפשר לומר שזה “המינוס של (שלוש פעמים חמש)”, כלומר קודם נכפול את שלוש בחמש “כרגיל”, נקבל 15, ואז נשים סימן מינוס לפני הכל. אם נעשה את זה על “מינוס שלוש פעמים מינוס חמש” נקבל \( -\left(-15\right) \), וכאן אנחנו עוברים לטענה שמינוס של מספר שהוא מינוס של מספר חיובי הוא המספר החיובי הזה. זה מזכיר את מה שכבר דיברנו עליו אבל לא לגמרי זהה, כי אני מבדיל בין פעולת החיסור בין שני מספרים ובין פעולת ה”מינוס על מספר בודד”. אז בואו ננסה לתת עוד אינטואיציה למהו בכלל מינוס של מספר.
על קומות וציר המספרים
חיפה היא עיר שחלקים נכבדים ממנה בנויים על הר. כתוצאה מכך יש לא מעט בניינים שיש להם כניסות שונות בגבהים שונים. בבניין שבו אני גר, למשל, יש כניסה אחת בקומה 0 וכניסה אחרת בקומה 6. הכניסה של קומה 6 היא הכניסה הראשית לבניין. אולי היה נכון יותר לומר שקומה 0 היא הקומה שבה הכניסה הראשית לבניין, ואז הקומות שמתחתיה יהיו קומות \( -1,-2 \) וכן הלאה, עד לקומה \( -6 \) שבה תהיה הכניסה התחתונה לבניין? זה האופן שבו אנחנו חושבים לפעמים על מספרים: יש לנו נקודת ייחוס, שיכולה להיות שרירותית מאוד, שאנחנו קוראים לה 0. אנחנו בוחרים כיוון (במקרה שלנו, “למעלה”) וככל שאנחנו מתקדמים בכיוון הזה, אנחנו מסמנים את ההתקדמות שלנו במספרים חיוביים. אם אנחנו נעים בכיוון ההפוך (“למטה” במקרה שלנו) אנחנו מסמנים את ההתקדמות שלנו במספרים שליליים. להגיד “קומה 3” זה כמו להגיד “הקומה שאם אתם נמצאים כרגע בקומה 0, עליכם לעלות 3 קומות כדי להגיע אליה” ולהגיד “קומה \( -6 \)” זה להגיד “הקומה שאם אתם נמצאים כרגע בקומה 0, עליכם לרדת 6 קומות כדי להגיע אליה”.
זה האופן שבו נבנה ציר המספרים. יש לנו נקודת התחלה שרירותית שאנחנו קוראים לה 0. לכל מה שמימין אליה אנחנו קוראים “מספרים חיוביים” ולכל מה שמשמאלה אנחנו קוראים “מספרים שליליים”. בצורת המבט הזו די ברור שיש כאן סימטריה - אין הבדל עקרוני בין צד ימין וצד שמאל. אז איך קורה שהסימטריה “נשברת” - ש”ימין כפול ימין” הוא “ימין” אבל “שמאל כפול שמאל” הוא גם כן “ימין”?
כמו קודם, אני חושב שהמפתח להבנה של מה שהולך פה הוא להפסיק לחשוב על כפל בתור פעולה סימטרית. כשאני אומר “\( a \) כפול \( b \)” יש הבדל בין התפקיד של \( a \) והתפקיד של \( b \). מבחינתי \( b \) היא נקודה כלשהי על ציר המספרים, ו-\( a \) הוא “הוראת עבודה” שמסבירה לי איך לייצר מתוך \( b \) נקודה אחרת על ציר המספרים. כפל ב-2, למשל, אומר “תסתכל על המרחק של \( b \) מראשית הצירים, ואז תלך את המרחק הזה פעמיים, באותו כיוון כמו \( b \) עצמה”. כפל ב-\( \frac{1}{2} \) אומר “תסתכל על המרחק של \( b \) מראשית הצירים ואז תלך חצי מהמרחק הזה, באותו כיוון כמו \( b \) עצמה” וכן הלאה. ומה זה כפל במינוס 1? זה להגיד “תסתכל על המרחק של \( b \) מראשית הצירים, ואז לך את המרחק הזה בכיוון ההפוך.” כלומר, כפל ב-\( a \) הוא הוראה שכוללת שני מרכיבים: פי כמה להגדיל/להקטין את המרחק של \( b \) מראשית הצירים, ובאיזה כיוון ללכת. האם ימינה או שמאלה. הכיוון הזה הוא יחסי - הוא נמדד ביחס ל-\( b \) עצמה. אם \( a \) חיובי, אז ההנחיה היא “לך כמו \( b \)” ואילו אם \( a \) שלילי ההנחיה היא “לך הפוך מ-\( b \)”. לכן, כשאני כופל שלילי בשלילי, אני אומר “לך הפוך מהכיוון של מספר שלילי” - כלומר, לך לכיוון החיובי. במילים אחרות, אני לא חושב שנכון לקרוא לכפל שלילי בשלילי בשם “שמאל כפול שמאל” אלא בשם “הפוך-כיוון כפול שמאל” (מה שיוצא כמובן “ימין”) בזמן ש”ימין כפול ימין” זה בעצם “הישאר באותו כיוון כפול ימין”, שגם הוא יוצא כמובן “ימין”.
אז איפה טמון חוסר הסימטריה? בכך שהחלטנו לשייך את הפעולה של “הפוך כיוון” יחד עם כפל במספר שלילי. אם יורשה לי להשתמש בעוד קצת טרמינולוגיה, המושג של “המרחק של \( b \) מראשית הצירים” נקרא ערך מוחלט של \( b \) ומסומן ב-\( \left|b\right| \). הערך המוחלט הוא תמיד מספר אי-שלילי; זו הייתה ההחלטה השרירותית ששברה את הסימטריה בין “ימין” ו”שמאל”.
בונוס למיטיבי לכת מתמטיים
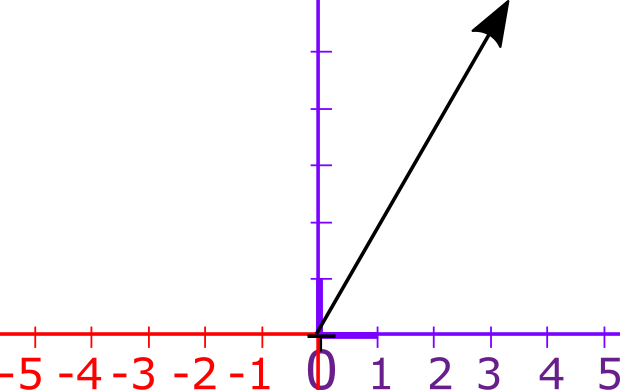
בואו נעזוב לרגע את ציר המספרים ונעבור לדבר על המישור הדו-ממדי. כל נקודה במישור הדו ממדי ניתנת לייצוג על ידי “וקטור” - חץ שיוצא מראשית הצירים ומגיע עד לנקודה הזו
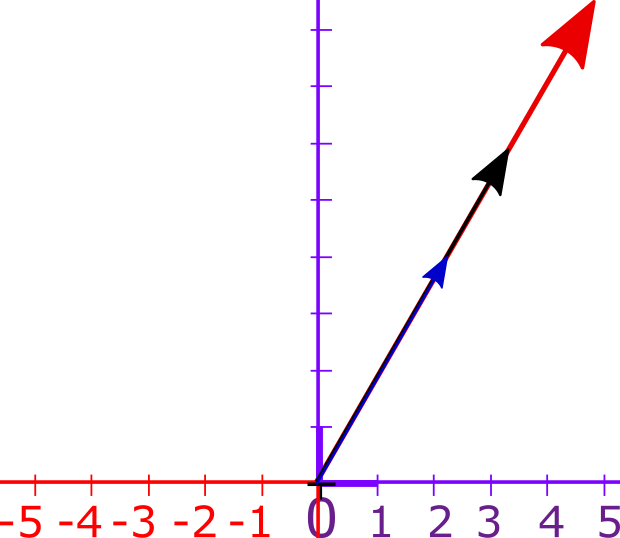
ציר המספרים הוא כמובן חלק מהמישור הדו-ממדי, אבל במישור הדו-ממדי אפשר לחשוב על עוד נקודות מלבד אלו שעל ציר המספרים. כעת, אילו פעולות ניתן לבצע על וקטורים במישור הדו ממדי? שתי פעולות שונות: ראשית, אפשר להאריך או לקצר את הוקטור:
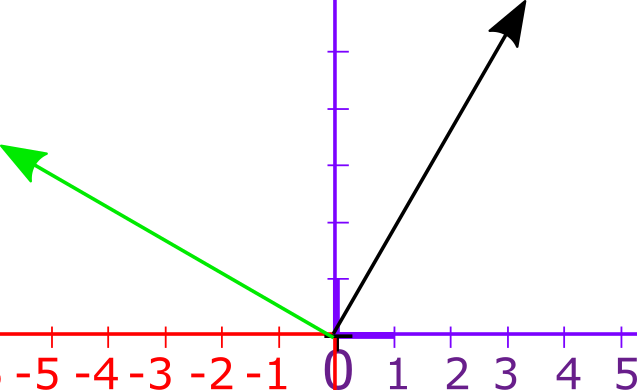
שנית, אפשר לסובב וקטור מבלי לשנות את האורך שלו. “כמות הסיבוב” הזו נקראת זווית. הנה סיבוב ב-90 מעלות של וקטור:
בגישה הזו אפשר לחשוב על כפל במינוס 1 בתור סיבוב ב-180 מעלות. בפרט, עבור וקטור שנח בצד הימני של ציר \( x \), הסיבוב הזה יעביר אותו לנקודה הסימטרית בצד השמאלי של ציר המספרים, וההפך. זה רק מקרה פרטי של ההגדרה הכללית: אפשר להגדיר את הכפל של הוקטור \( v \) בוקטור \( u \) על ידי “כפול את האורך של \( v \) באורך של \( u \) וסובב את \( v \) באותה זווית סיבוב ש-\( u \) יוצר עם ציר \( x \)”. ההגדרה הזו פשוט מושלמת, לטעמי, כי בה סוף סוף חוזרת הסימטריה לפעולת הכפל שלנו. התוצאה של הכפלת \( u \) ב-\( v \) היא וקטור שהאורך שלו הוא המכפלה של האורכים של \( u,v \) (מכפלה של מספרים אי-שליליים ולכן כזו שהסימטריה בה מובהקת), והזווית שלו היא סכום הזוויות של \( u,v \) (חיבור של מספרים אי-שליליים ולכן כזה שהסימטריה בו מובהקת). אני יכול לגלות לכם עכשיו שמערכת המספרים ה”מושלמת” הזו שבה מככבים הוקטורים הללו נקראת המספרים המרוכבים - על כל מספר מרוכב אכן אפשר לחשוב בתור וקטור עם אורך וזווית (בהקשר של מרוכבים זה נקרא “הערך המוחלט” וה”ארגומנט” של המספר המרוכב) והדרך שבה מתייחסים לכפל מרוכבים היא בדיוק זו - מכפלת ערכים מוחלטים, חיבור הארגומנט.
ומה עם הגישה האקסיומטית?
הבטחתי בתחילת הפוסט שאסביר גם למה “זה נובע מהתכונות הבסיסיות של כפל וההגדרה של שליליים” זו התשובה הנכונה מבחינה מתמטית כאן, אז בואו נראה על אילו תכונות בסיסיות של כפל מדובר. התכונה המהותית ביותר של כפל מבחינתנו היא זו שמחברת אותו לחיבור - מה שנקרא “חוק הפילוג” שאומר שמתקיים \( a\times\left(x+y\right)=a\times x+a\times y \) (ואם חוק החילוף לא מתקיים גם דורשים מפורשות את ההפך, \( \left(x+y\right)\times a=x\times a+y\times a \). פרט לכך אנחנו צריכים את ההגדרה של מספר נגדי: אם \( a \) הוא מספר כלשהו, אז הנגדי שלו מסומן ב-\( -a \) והוא המספר המקיים \( a+\left(-a\right)=0 \). גם ל-0 עצמו יש חשיבות: הוא המספר שמקיים \( a+0=a \) לכל \( a \). עכשיו אפשר לקחת את כל אלו ולהתחיל להסיק מהם מסקנות.
ראשית, הנגדי של \( a \) הוא יחיד, מה שמצדיק שימוש במילה כמו “ה”נגדי, עם ה’ הידיעה. למה? כי אם \( a+x=0 \) וגם \( a+y=0 \) אז \( a+x=a+y \). נחבר \( x \) משמאל לשני האגפים ונקבל \( 0+x=0+y \), כלומר \( x=y \). שימו לב לתעלול הזה של “חיבור נגדי לשני האגפים” - אנחנו מכירים אותו פשוט בתור “להעביר אגף ולצמצם” וזה מה שאעשה מעתה. כעת, המסקנה מהיחידות הזו היא שהנגדי של הנגדי הוא המספר המקורי. כלומר, \( -\left(-a\right)=a \).
שנית, כפל ב-0 חייב להחזיר 0, כלומר \( a\times0=0 \). למה? כי \( a\times0=a\times\left(0+0\right)=a\times0+a\times0 \). על ידי צמצום נקבל \( a\times0=0 \).
כעת נחשב את \( a\times\left(x+\left(-x\right)\right) \) בשתי דרכים שונות. ראשית, על פי הגדרת נגדי, \( a\times\left(x+\left(-x\right)\right)=a\times0=0 \). שנית, על פי חוק הפילוג נקבל \( a\times\left(x+\left(-x\right)\right)=a\times x+a\times\left(-x\right) \). מכיוון שכל זה שווה ל-0, נעביר אגף ונקבל \( a\times\left(-x\right)=-\left(a\times x\right) \).
לא קשה להראות שאותו תעלול עובד עם עבור \( \left(-x\right)\times b=-\left(x\times b\right) \). אם נשלב את שני אלו, נקבל:
\( \left(-a\right)\times\left(-b\right)=-\left(-\left(-a\right)\times\left(-b\right)\right)=-\left(a\times\left(-b\right)\right)= \)
\( =-\left(-\left(a\times\left(-\left(-b\right)\right)\right)\right)=-\left(-\left(a\times b\right)\right)=a\times b \)
וזה מסיים את ההוכחה הפורמלית. במילים אחרות, אם האינטואיציה שלכם מקבלת את ההגדרה של שלילי ואת חוק הפילוג, אני לא רואה למה לא להמשיך עם הלוגיקה הזו ולהסכים לכך ששלילי כפול שלילי הוא חיובי.
נהניתם? התעניינתם? אם תרצו, אתם מוזמנים לתת טיפ: