בואו נפתור את הבגרות במתמטיקה! (חלק ב')

אני ממשיך את מה שעשיתי בפוסט הקודם - פותר בחינת בגרות במתמטיקה, והפעם את חלק ב’ שלה. והפעם, כבונוס, אני מתאר שתי טעויות מביכות במיוחד שהיו לי בפתרונות ולא שמתי לב אליהן בזמן אמת!

הבגרות היא שאלון 317 של קיץ 2016.

שאלה 1

אה, גאומטריה אנליטית. זה הולך להיות מעניין. מצד אחד, זה תחום חשוב ומועיל ואהבתי אותו בבית הספר ואני גם סוג של משתמש בו פה ושם בימינו. מצד שני, אני בטוח שאני לא שולט בכל מה שצריך בשביל לפתור מבחן בבית הספר (מעולם לא למדתי אליפסות, למשל). בואו נראה איך אסתדר.

סעיף א

יש לי בעיה כבר ברמת הטקסט הבסיסי: אין לי מושג מה זה “מדריך הפרבולה”, אז אין לי מושג איך מוצאים את נקודת החיתוך שלו עם ציר \( x \). אז אני מגגל ונזכר בהגדרות: פרבולה עם משוואה \( y^{2}=2px \) היא אוסף הנקודות שהמרחק שלהן מקו אנכי שנקרא “מדריך הפרבולה” ומנקודה על ציר \( x \) (“מוקד הפרבולה”) שווים. ה-\( p \) שבנוסחת הפרבולה הוא המרחק בין המדריך והמוקד, והרעיון הוא שהפרבולה עוברת בראשית הצירים וברביעים 1 ו-4, כלומר המוקד נמצא ב-\( \frac{p}{2} \) ואילו המדריך עובר דרך \( -\frac{p}{2} \) ולכן המשוואה שלו היא \( x=-\frac{p}{2} \). במילים אחרות, \( A=\left(-\frac{p}{2},0\right) \).

עכשיו, איך אני מוצא משיק לפרבולה בנקודה כלשהי? בטח נתנו נוסחה של זה בדף הנוסחאות, אבל למה שלא אנסה להמציא מחדש בעצמי. שיפוע המשיק לפונקציה כלשהי בנקודה מסויימת הוא הנגזרת של הפונקציה באותה נקודה. כאן יש לנו פרבולה שהיא לא בדיוק פונקציה אלא הדבקה של שתי פונקציות: \( y=\sqrt{2px} \) ו-\( y=-\sqrt{2px} \). אפשר לגזור אותן וכאלה, אבל אני מכיר רמאות טכנית - אפשר גם לגזור את \( y^{2}=2px \) בצורה סתומה, ומקבלים \( 2y\cdot y^{\prime}=2p \), כלומר \( y^{\prime}=\frac{p}{y} \). אפשר להציב במקום \( y \) את \( \pm\sqrt{2px} \) אבל אני חושד שכרגע עם \( y \) זה יהיה יותר מועיל לי. על טריקים כמו הגזירה הסתומה הזו אני אומר - ילדים, אל תנסו את זה בבית! יש הסבר מלא לתעלול הזה ויש לי פוסט בבלוג עליו, אבל זה לא נושא שקל להבין.

עכשיו, נניח שיש לנו ישר שעובר דרך \( \left(x_{0},y_{0}\right) \) וגם דרך \( A=\left(-\frac{p}{2},0\right) \). מה השיפוע שלו? באופן כללי השיפוע של ישר שעובר דרך \( \left(x_{1},y_{1}\right) \)ו-\( \left(x_{2},y_{2}\right) \) הוא \( m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}} \), ולכן כאן הוא יהיה \( m=\frac{y_{0}}{x_{0}+\frac{p}{2}} \). יש לנו כבר ביטוי אחר לשיפוע שקיבלנו מתוך הגזירה של הפרבולה: \( m=\frac{p}{y_{0}} \). נשווה את שני אלו ונקבל:

\( \frac{p}{y_{0}}=\frac{y_{0}}{x_{0}+\frac{p}{2}} \)

כלומר:

\( y_{0}^{2}=p\left(x_{0}+\frac{p}{2}\right) \)

עכשיו, אנחנו יודעים ש-\( y_{0}^{2}=2px_{0} \), כלומר קיבלנו:

\( 2px_{0}=p\left(x_{0}+\frac{p}{2}\right) \)

ועל כן:

\( 2px_{0}-px_{0}=\frac{p^{2}}{2} \)

כלומר

\( x_{0}=\frac{p}{2} \)

הגענו לשוויון הזה מתוך משוואה שההנחות היחידות שלה היו שהישר שלנו משיק לפרבולה ועובר דרך \( A \). ההנחות הללו הכריחו את קואורדינטת ה-\( x \) של נקודת ההשקה להיות \( \frac{p}{2} \), וזה מסיים את הדבר הראשון שהיה צריך להראות.

הדבר השני, כרגיל בבגרות, לא באמת נכון בלי הנחה נוספת שהיא אולטרה-קטנונית - ששתי נקודות ההשקה לפרבולות שונות, כלומר שהמשיקים שונים זה מזה. מן הסתם אני מניח את זה בלי להניד עפעף. מה זה אומר? זה אומר שנקודות ההשקה חייבות לקיים \( y_{0}=\sqrt{2px_{0}}=p \) עבור אחת מהן, ו-\( y_{0}=-\sqrt{2px_{0}}=-p \) עבור השניה. זה ישפיע על השיפועים של המשיקים הללו. כדי לראות שהם מאונכים זה לזה, צריך לכפול את השיפועים ולראות שהם שווים \( -1 \). רגע, מאיפה אני יודע את זה בכלל? נראה לי שזה זכרון עמום מימי התיכון שלי. למה שזה יהיה נכון? ובכן, מה זה “שיפוע” אצלנו? זה טנגנס הזווית שהישר יוצר עם ציר ה-\( x \) (את זה קל לי לזכור כי אני זוכר שב-\( 90^{\circ} \) השיפוע הוא “אינסוף”). גיגול זריז נותן לי את הנוסחה למכפלת טנגנסים וקל לראות בה שאם ההפרש בין שתי זוויות הוא \( 90^{\circ} \) אז מכפלת הטנגנסים תצא מינוס 1 (אלא אם השיפוע הוא “אינסוף”) - לא אלאה אתכם בזה, ממילא זו אקסיומה שכזו בתיכון. בקיצור, אני רוצה לבדוק את ערך המכפלה \( \frac{p}{p}\cdot\frac{p}{-p} \) שכמובן שווה \( -1 \). קיבלתי את המבוקש. יאיי! לא חשבתי שאצליח.

סעיף ב'

עכשיו נותנים לנו גם מעגל עם מרכז בנקודה \( M=\left(x_{M},0\right) \) ומבקשים מאיתנו למצוא את המשוואה שלו - כלומר, צריך למצוא את \( x_{M} \) ואת הרדיוס. הנתון שלנו הוא שהמשיקים לפרבולה משיקים גם למעגל באותן נקודות. אז נראה לי שהגיע הזמן לכתוב במפורש מהן הנקודות. אמרו לנו ש-\( p=2 \), אז נקודות ההשקה הן

\( K=\left(1,2\right),L=\left(1,-2\right) \).

יש לי שתי נקודות על המעגל. האם זה מספיק לי כדי למצוא את המשוואה שלו או שאצטרך להשתמש גם בכך שהמשיקים לפרבולה משיקים למעגל ולא סתם חותכים אותו? בואו ננסה קודם לעבוד עם מה שיש. כרגע משוואת המעגל היא \( \left(x-x_{M}\right)^{2}+y^{2}=R^{2} \). מכיוון ש-\( y \) מופיע רק בריבוע, הצבה של \( K \) והצבה של \( L \) למשוואה הזו יתנו לי את אותו דבר בדיוק: \( \left(1-x_{M}\right)^{2}+4=R^{2} \). זה לא מספיק טוב, צריך עוד משוואה.

אם כן, מהו השיפוע של משיק למעגל? נגזור שוב באופן סתום ונקבל \( 2\left(x-x_{M}\right)+2yy^{\prime}=0 \), כלומר \( y^{\prime}=-\frac{x-x_{M}}{y} \). כבר ראינו שהשיפוע של הישרים שלנו הוא \( 1,-1 \) ולכן בואו ננסה להציב אחד מהם:

\( 1=-\frac{1-x_{M}}{2} \)

וקיבלנו ש-\( x_{M}=3 \). נציב את זה במשוואה \( \left(1-x_{M}\right)^{2}+4=R^{2} \) ונקבל \( R^{2}=8 \). כלומר, משוואת המעגל היא \( \left(x-3\right)^{2}+y^{2}=8 \).

סעיף ג'

עכשיו מגיע עוד משהו שאין לי מושג איך עושים - משוואת מעגל שחסום במרובע. כרגיל, אני מעדיף לנסות להמציא מחדש את הגלגל במקום להסתכל בדף נוסחאות או משהו דומה. אני אומר - משוואת מעגל כללית היא \( \left(x-x_{0}\right)^{2}+\left(y-y_{0}\right)^{2}=R^{2} \). גוזרים ומקבלים ש-\( 2\left(x-x_{0}\right)+2\left(y-y_{0}\right)y^{\prime}=0 \), כלומר ש-\( y^{\prime}=-\frac{x-x_{0}}{y-y_{0}} \) היא המשוואה לשיפוע המשיק שעובר דרך \( \left(x,y\right) \). אם המעגל חסום במרובע זה נותן לי ארבעה משיקים שאני מכיר. בואו ננסה לעשות סדר ולכתוב הכל במפורש:

\( A=\left(-1,0\right) \)

\( M=\left(3,0\right) \)

\( K=\left(1,2\right) \)

\( L=\left(1,-2\right) \)

\( \text{AK: }y=x+1 \)

\( \text{KM: }y=-x+3 \)

\( \text{ML: }y=x-3 \)

\( \text{LA: }y=-x-1 \)

מהמשוואות ברור שזה לא סתם מרובע אלא מלבן, כי הצלעות ניצבות זו לזו. מדידת אורכי הצלעות מראה שזה ריבוע עם אורך צלע 2. האם זה עוזר לי איכשהו? סביר להניח שכן - הסימטריה גוררת שמרכז המעגל יהיה גם מרכז הריבוע. האם מותר לי להשתמש בשיקולי סימטריה שכאלו פה? בואו נניח שכן כי אין לי מושג איך לפתור אחרת. בעזרת סימטריה כל מה שאני צריך לעשות הוא למצוא את מרכז הריבוע. הדרך שנראית לי הכי בטוחה לעשות את זה היא למצוא את האלכסונים \( \text{AM} \) ו-\( \text{KL} \) ולבדוק מהי נקודת החיתוך שלהם. המשוואות שלהם הן \( y=0 \) ו-\( x=1 \), כך שנקודת החיתוך היא פשוט ב-\( \left(1,0\right) \). והרדיוס? מספיק לי לחשב את המרחק מ-\( \left(1,0\right) \) לאמצע של אחת מצלעות הריבוע, נאמר אל \( \left(0,1\right) \) שהוא אמצע הצלע \( \text{AK} \). המרחק בבירור מקיים \( R^{2}=2 \), כך שמשוואת המעגל היא \( \left(x-1\right)^{2}+y^{2}=2 \).

מה דעתי על השאלה?

לטעמי זו שאלה טובה, אם מקבלים את זה שכדאי ללמוד גאומטריה אנליטית, ולדעתי כדאי ללמוד גאומטריה אנליטית. אבל קצת הפריע לי שאין לי מושג איך פותרים את ג’ בדרך כללית, אם זה אפשרי בכלל. לא כי זה פוגם בשאלה עבורי, אלא כי אני לא בטוח מה תלמיד בית ספר עושה כשהוא צריך להתמודד עם שאלה כמו זו.

שאלה 2

הא, שאלת וקטורים. הנה וידוי אפל: זו לא הפעם הראשונה שבה השתעשעתי במחשבה על כתיבת פוסט פתרון בגרות. בפעם הקודמת ניגשתי לבגרות אקראית, ניסיתי קודם כל לפתור את שאלת הוקטורים שלהם, כי “פחחח זה כמו אלגברה לינארית אני אוכל את זה בלי מלח”, ואז לא הצלחתי לפתור אותה. בכלל. בואו נראה אם זה מה שיקרה גם הפעם…

סעיף א'

להודות על האמת? גם הפעם אין לי מושג איך אמורים לפתור את השאלה הזו. וקטורים זה לא נושא שלמדתי אי פעם בתיכון. אבל איך אני פותר את השאלה? ובכן, בנקודה שבה הישר משיק למעגל הרדיוס של המעגל מאונך אליו. בהינתן ישר ונקודה, האנך לישר הזה שעובר דרך הנקודה הוא המרחק של הנקודה מהישר - האורך של האנך הוא המינימלי מבין אורכי כל הקווים מהנקודה אל הישר. אז יש לנו פה בעיית מינימיזציה פשוטה. נגדיר פונקציה

\( f\left(t\right)=\left|B-O\right|^{2}=\left|\left(2+t,2+2t,t\right)-\left(0,0,0\right)\right|=\left(2+t\right)^{2}+\left(2+2t\right)^{2}+t^{2}=6t^{2}+6t+8 \)

נגזור ונקבל \( f^{\prime}\left(t\right)=6t+6 \). נשווה לאפס ונקבל \( t=-1 \). לכן \( B=\left(2-1,2-2,-1\right)=\left(1,0,-1\right) \).

זה היה מאוד קל, אבל השתמשתי פה בחדו”א; אני מנחש שבתיכון לומדים את הנוסחה למרחק נקודה מישר או משהו ומשתמשים בזה.

סעיף ב'

נתחיל בלנסות להבין איך בדיוק נראה המעגל. מה הרדיוס שלו? אנחנו יודעים ש-\( B=\left(1,0,-1\right) \) נמצאת על המעגל, כך שרדיוס המעגל הוא \( \sqrt{1^{2}+0^{2}+\left(-1\right)^{2}}=\sqrt{2} \). אם נמצא את \( A \) ונראה שזה המרחק שלה מראשית הצירים, סיימנו. אבל איך עושים את זה? צריך למצוא את המישור \( \pi \) איכשהו. נתונים לנו שני ישרים במישור: \( l_{1} \) וגם הרדיוס של המעגל. המישור גם עובר דרך ראשית הצירים אז אין צורך להזיז אותו במיוחד (על ידי חיבור של נקודה שונה מאפס אל הצירוף הלינארי של שני הישרים הללו). כעת, את הישר \( l_{1} \) נזיז אל ראשית הצירים ונקבל את הוקטור \( \left(1,2,1\right) \). הרדיוס מתואר על ידי הוקטור \( \left(1,0,-1\right) \) (שהוא בעצם הנקודה \( B \)). לכן משוואת המישור היא \( \pi:t_{1}\left(1,2,1\right)+t_{2}\left(1,0,-1\right) \). אנחנו רוצים למצוא חיתוך בין זה ובין \( \left(0,1,1\right)+s\left(2,-1,1\right) \). כלומר, יש לנו מערכת משוואות בשלושה נעלמים \( \left(t_{1},t_{2},s\right) \) ועם שלוש משוואות (עבור קואורדינטות \( x,y,z \)). אפשר לכתוב זאת כך: \( t_{1}\left(1,2,1\right)+t_{2}\left(1,0,-1\right)=s\left(2,-1,1\right)+\left(0,1,1\right) \) ואחרי העברת אגפים נקבל \( t_{1}\left(1,2,1\right)+t_{2}\left(1,0,-1\right)+s\left(-2,1,-1\right)=\left(0,1,1\right) \).

ברשותכם אכתוב את זה כמטריצה:

\( \left(\begin{array}{ccc}1 & 1 & -2\\2 & 0 & 1\\1 & -1 & -1\end{array}\right)\left(\begin{array}{c}t_{1}\\t_{2}\\s\end{array}\right)=\left(\begin{array}{c}0\\1\\1\end{array}\right) \)

נחסיר את השורה הראשונה משתי האחרות (מהשניה, כשהראשונה מוכפלת פי 2) ונקבל

\( \left(\begin{array}{ccc}1 & 1 & -2\\0 & -2 & 5\\0 & -2 & 1\end{array}\right)\left(\begin{array}{c}t_{1}\\t_{2}\\s\end{array}\right)=\left(\begin{array}{c}0\\1\\1\end{array}\right) \)

עכשיו נשתמש בשורה השלישית כדי לאפס את הקואורדינטה השניה בשתי האחרות:

\( \left(\begin{array}{ccc}1 & 0 & -\frac{3}{2}\\0 & 0 & 4\\0 & 1 & -\frac{1}{2}\end{array}\right)\left(\begin{array}{c}t_{1}\\t_{2}\\s\end{array}\right)=\left(\begin{array}{c}\frac{1}{2}\\0\\-\frac{1}{2}\end{array}\right) \)

בגלל שקיבלנו 0 בעמודת התוצאה בשורה השניה אנחנו יכולים להשתולל איתה חופשי ולאפס את שאר השורות בקואורדינטה הזו בלי לשנות את התוצאה. נקבל:

\( \left(\begin{array}{ccc}1 & 0 & 0\\0 & 0 & 1\\0 & 1 & 0\end{array}\right)\left(\begin{array}{c}t_{1}\\t_{2}\\s\end{array}\right)=\left(\begin{array}{c}\frac{1}{2}\\0\\-\frac{1}{2}\end{array}\right) \)

הפתרון פה הוא חד משמעי: \( t_{1}=\frac{1}{2},t_{2}=-\frac{1}{2} \) ו-\( s=0 \). מה שנחמד הוא שקל לבדוק את הפתרון הזה במפורש על ידי הצבה:

\( \frac{1}{2}\left(1,2,1\right)-\frac{1}{2}\left(1,0,-1\right)+0\left(-2,1,-1\right)=\left(\frac{1}{2}-\frac{1}{2},1-0,\frac{1}{2}+\frac{1}{2}\right)=\left(0,1,1\right) \), כמבוקש.

קיבלנו, אם כן, שנקודת החיתוך היא \( A=\left(0,1,1\right) \) עצמה. מכיוון ש-\( \left|\left(0,1,1\right)-\left(0,0,0\right)\right|=\sqrt{2} \) קיבלנו שהיא אכן על המעגל. נותר רק למצוא את השטח של המשולש \( \text{AOB} \). וזו שאלה מעניינת בפני עצמה בשבילי - איך מוצאים שטח של משולש בתלת מימד כשנתונות לי רק הקואורדינטות של הקודקודים שלו? אני זוכר במעורפל שזה קשור למכפלה וקטורית (ליתר דיוק, אני זוכר שזו מכפלת אורכי הוקטורים בסינוס הזווית ביניהם ואני זוכר שהדבר הזה הוא מכפלה וקטורית), ובדיקה זריזה מעלה שאכן כך הדבר - מכפילים וקטורית שתי צלעות של המשולש, לוקחים את גודל הוקטור שהתקבל, מחלקים ב-2. אויש, אני שונא מכפלות וקטורית. טוב, בואו נעשה את זה, אני זוכר את “שיטת הדטרמיננטה” לחישוב:

\( \left|\begin{array}{ccc}\hat{x} & \hat{y} & \hat{z}\\1 & 0 & -1\\0 & 1 & 1\end{array}\right|=1\cdot\hat{x}-1\cdot\hat{y}+1\cdot\hat{z} \)

ולכן קיבלנו שטח של \( \frac{\sqrt{1^{2}+1^{2}+1^{2}}}{2}=\frac{\sqrt{3}}{2} \).

מה דעתי על השאלה?

בכל הנושא הזה של וקטורים יש לי תחושה ש”עוברים ליד” אלגברה לינארית אבל לא באמת נוגעים בה - לא באמת יצא לי לפתור תרגילים כמו זה אי פעם. מצד שני, אלגברה לינארית מופשטת יותר זה משהו שכנראה אי אפשר ללמד בבית הספר, ואילו החומר הזה נראה לי אפילו שימושי למי שהולכים לתחומים יותר פיזיקליים/הנדסיים באופיים. קשה לי להתלונן.

שאלה 3

סעיף א'

נתון לנו מספר מרוכב מחריד, אבל מן הסתם אפשר לפשט אותו. אני לא זוכר מתי לאחרונה כתבתי \( \text{CIS} \) ואין לי כוונה להתחיל עכשיו - אשתמש בסימון הסטנדרטי יותר במתמטיקה, \( e^{i\theta}=\cos\theta+i\sin\theta \). בסימון הזה המונה הוא \( e^{i\left(\pi/9\right)} \) ואילו המכנה הוא… אה, יש מינוס ליד הסינוס. זה אומר שלוקחים מינוס של כל הזווית, כלומר המכנה הוא \( e^{-i\left(\pi/12\right)} \). עכשיו קל לבצע העלאה בחזקה - פשוט כופלים את המעריך של האקספוננט בחזקה הזו, כמו בחוקי חזקות רגילים, וגם חלוקה מתבצעת בדרך דומה:

\( z=\frac{\left(e^{i\frac{\pi}{9}}\right)^{3}}{\left(e^{-i\frac{\pi}{12}}\right)^{2}}=\frac{e^{i\frac{\pi}{3}}}{e^{-i\frac{\pi}{6}}}=e^{i\left(\frac{\pi}{3}+\frac{\pi}{6}\right)}=e^{i\frac{\pi}{2}} \)

כעת, \( \left|z\right|=1 \) (כי ה-\( e \) בחזקת \( i \)-משהו לא מוכפל בשום מספר ממשי שונה מ-1) ואילו הארגומנט של \( z \) הוא \( \frac{\pi}{2} \).

קל לחשב את החזקה \( z^{n} \) כעת: \( z^{n}=e^{i\frac{n\pi}{2}} \). כדי לקבל מספר מדומה טהור, הארגומנט מודולו \( 2\pi \) צריך להיות \( \frac{\pi}{2} \) או \( \frac{3\pi}{2} \) (אני זוכר את זה גאומטרית - צריך שהסיבוב של המספר המרוכב ביחס לציר \( x \) יהיה של 90 מעלות או 270 מעלות, כך שנחים על ציר \( y \)). כלומר, \( n\equiv1,3\left(\text{mod }4\right) \), או בסימון שאולי יותר אוהבים בתיכון - \( n=1+4k \) או \( n=3+4k \) (למעשה, זו דרך מסורבלת לומר ש-\( n \) אי זוגי, אבל זה מה שקפץ לי לראש ולא ניסיתי לפשט).

סעיף ב'

ממבט חטוף על המקום הגאומטרי אין לי מושג קלוש מה הוא. אז בואו ננסה לפשט. אני זוכר את הנוסחאות החביבות הבאות: \( z+\overline{z}=2\text{Re}z \) ו-\( z-\overline{z}=2\text{Im}z \). אם כן, אפשר לכתוב את המקום הגאומטרי גם בתור \( \left|\text{Re}z-m\text{Im}z\right|=20 \).

רגע, לא, פסק זמן.

לכתוב \( \left|\text{Re}z-m\text{Im}z\right|=20 \) זה שגוי לגמרי ואני עשיתי את הטעות הזו בכל זאת ופתרתי את התרגיל על פי זה וקיבלתי פתרון שגוי. אחסוך מכם את הפתרון הזה. יש לנו כאן דוגמה קלאסית לפאשלת חוסר תשומת לב של “כן, ברור שאני יודע את זה”. איפה טעיתי? הנוסחה \( z-\overline{z}=2\text{Im}z \) לא נכונה; מה שנכון הוא \( z-\overline{z}=2i\cdot\text{Im}z \). כלומר, זה מוכפל ב-\( i \), מה שמשנה לגמרי את ההמשך. אוי ווי. בכל מה שקרה אחרי הטעות הזו לא פקפקתי בכלל במה שכתבתי ולא היה לי איך לבדוק את עצמי. פשוט פאשלה מביכה.

אוקיי, עכשיו משעליתי על הטעות בדיעבד, מה הפתרון הנכון? ובכן, חזרה אל הנוסחה שהגענו אליה: \( \left|\text{Re}z-mi\cdot\text{Im}z\right|=20 \). בואו נחשוב על \( z \) בתור נקודה ב-\( \mathbb{R}^{2} \), כלומר במקום לכתוב \( z=x+iy \) נכתוב \( \left(x,y\right) \). אז הנוסחה היא \( \left|x-miy\right|=20 \), ועל פי נוסחת הערך המוחלט של מרוכבים זה אומר \( x^{2}+\left(my\right)^{2}=400 \). זה נראה כמו משוואת מעגל מוזרה - בפועל אני יודע שזו משוואת אליפסה, אבל גם שדרך ההצגה הזו היא לא דרך ההצגה ה”סטנדרטית” של משוואת אליפסה. הייתי צריך להזכיר לעצמי (על ידי גיגול) שהמשוואה של אליפסה שהצירים שלה נמצאים על צירי \( x,y \) היא \( \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1 \) כאשר \( a,b \) הם פרמטרים של האליפסה: נקודות החיתוך של האליפסה עם הצירים הן בדיוק \( \pm\left(a,0\right) \) ו-\( \pm\left(0,b\right) \). במקרה הנוכחי, אם כן, נחלק ב-\( 20^{2} \) את שני האגפים ונקבל \( \frac{x^{2}}{20^{2}}+\frac{y^{2}}{\left(20m^{-1}\right)^{2}}=1 \), דהיינו אצלנו \( a=20 \) ו-\( b=\frac{20}{m} \).

מה שמבקשים מאיתנו כעת הוא למצוא את \( a,b \) בהינתן שהנקודה \( \left(12,8\right) \) נמצאת על האליפסה. בפועל אני צריך למצוא את \( m \) כך שיותר קל לי לחזור למשוואה \( x^{2}+\left(my\right)^{2}=400 \). נציב את \( x,y \) ונקבל \( 144+64m^{2}=400 \), כלומר \( 9+4m^{2}=25 \) (עשיתי את החישובים בראש! הא!), כלומר \( m^{2}=4 \), כלומר \( m=2 \) (לא ייתכן ש-\( m=-2 \) כי אמרו לנו במפורש שהוא חיובי). מכאן ש-\( a=20,b=10 \) ולכן נקודות החיתוך הן \( \left(20,0\right),\left(-20,0\right),\left(0,10\right),\left(0,-10\right) \).

מה דעתי על השאלה?

האמת, לא משהו. וזה לא קשור לכך שבסעיף ב’ טעיתי באופן מזעזע ומביך! נשבע!

הבעיה בשאלה הזו היא שהיא כמעט לא עוסקת במספרים מרוכבים. טוב, בסעיף א’ צריך להבין את ההצגה הקוטבית של מספרים מרוכבים וכפועל יוצא מכך את כללי ההעלאה בחזקה והחילוק, אבל בסעיף ב’ כל מה שצריך לדעת הוא את ההגדרה של ערך מוחלט ואת הנוסחאות הללו לסכום והפרש עם הצמוד (כפי שראינו, גם אני לא באמת זכרתי אותן…). מעבר לכך רוב סעיף ב’ הוא בכלל שאלה נוספת בגאומטריה אנליטית (באופן חוקי מותר להם לעשות את זה ; הפרק כולו עוסק בגאומטריה אנליטית ומרוכבים, אין התחייבות לשאלה אחת על זה ושאלה אחרת על ההוא).

מצד שני, אולי זה בעצם בסדר? על מה בדיוק אפשר לשאול כשמדובר על מספרים מרוכבים מעבר לרמת ההגדרות הבסיסיות? משפט אינטגרל קושי? ואני כן חושב שכדאי לראות מספרים מרוכבים בבית הספר כדי להיות מודעים לקיום היצורים הללו. אז יש סיכוי טוב שאני מתלונן על כלום.

שאלה 4

הא. שוב חדו”א. אף פעם לא הבנתי למה יש שני סוגי חדו”א בבגרות. כאילו, מה כבר ההבדל הגדול בין שניהם?

סעיף א'

כבר התחלה טובה - אין לי מושג איך מוצאים את נקודות החיתוך עם הצירים של \( f\left(x\right)=9^{x}-2\cdot3^{x}-3 \). טוב, שניה, בואו לא נתייאש כל כך מהר. מה שמייד קופץ לי לעיניים הוא ש-\( 9=3^{2} \) כך שאפשר לכתוב \( f\left(x\right)=\left(3^{x}\right)^{2}-2\cdot3^{x}-3 \). קיבלנו פה משוואה ריבועית במשתנה \( t=3^{x} \), כלומר \( t^{2}-2t-3=0 \). את זה קל לי לפתור ולקבל \( t_{1,2}=\frac{2\pm\sqrt{4+12}}{2}=\frac{2\pm4}{2}=1\pm2=3,-1 \). עבור\( 3^{x}=3 \) הפתרון הוא כמובן \( x=1 \); ואילו למשואוה \( 3^{x}=-1 \) אין פתרון. לכן יש נקודת חיתוך יחידה עם הצירים: \( x=1 \).

עכשיו לאסימפטוטה אופקית. מה זו אסימפטוטה אופקית? אני מניח שהכוונה לקו האופקי (\( y=c \) עבור \( c \) כלשהו) שהפונקציה שואפת אליו כש-\( x \) שואף לאינסוף או מינוס אינסוף. כש-\( x \) שואף לאינסוף בבירור הפונקציה שואפת לאינסוף, אבל כשהוא שואף למינוס אינסוף אז \( 9^{x}\to0 \) וגם \( 3^{x}\to0 \) ולכן נקבל שאיפה ל-\( -3 \). כלומר, \( y=-3 \) הוא האסימפטוטה.

בשביל נקודות קיצון צריך לגזור. העניין הוא שאני לא זוכר איך גוזרים פונקציה מעריכית. אני זוכר ש-\( \left(e^{x}\right)^{\prime}=e^{x} \), אבל לא מה קורה כשהבסיס הוא \( a \). טוב, אני משקר, אני כן זוכר במעורפל שכופלים ב-\( \ln a \) אבל אני לא בטוח בזה. אפשר לבדוק בדף נוסחאות ואפשר לפתח את זה מחדש. אני יודע ש-\( e^{\ln a}=a \) כי זו ההגדרה של \( \ln \) פחות או יותר (האמת שמבחינתי ההגדרה של \( \ln x \) היא משהו מפלצתי עם אינטגרלים אבל נעזוב את זה). לכן \( a^{x}=\left(e^{\ln a}\right)^{x}=e^{x\ln a} \) ומכאן ברור ש-\( \left(a^{x}\right)^{\prime}=\left(e^{x\ln a}\right)^{\prime}=\ln a\cdot\left(e^{x\ln a}\right)=a^{x}\ln a \). יופי, אז בואו נגזור:

\( f^{\prime}\left(x\right)=2\cdot3^{x}\cdot3^{x}\cdot\ln3-2\cdot3^{x}\cdot\ln3=2\ln3\left(\left(3^{x}\right)^{2}-3^{x}\right) \)

שוב אסמן \( t=3^{x} \) ואקבל שהנגזרת מתאפסת אם \( t^{2}=t \), כלומר כש-\( t=0 \) (לא הולך לקרות עבור \( t=3^{x} \)) או אם \( t=1 \), מה שקורה כש-\( x=0 \). אז \( 0 \) היא נקודת קיצון, אבל האם מינימום או מקסימום? לפני שאני מחשב נגזרת שניה וכאלה בואו נחשוב רגע - כאשר \( x \) הולך וגדל גם הפונקציה הולכת וגדלה. לכן אם כבר יש פה נקודת קיצון היא תהיה נקודת מינימום. כש-\( x=0 \) הערך של הפונקציה הוא \( 1-2-3=-4 \) וכשאיקס שואף למינסוף אינסוף הפונקציה שואפת ל-\( -3 \), כך שגם זה עוזר לי לראות שיש פה מינימום. והנגזרת השניה? היא \( 2\ln3\left(2\ln3\cdot\left(3^{x}\right)^{2}-\ln3\cdot3^{x}\right)=2\ln^{2}3\left(2\left(3^{x}\right)^{2}-3^{x}\right) \) ולכן כשנציב \( x=0 \) נקבל משהו חיובי - מתאים לכך שזו נקודת מינימום. שימו לב שהנגזרת השניה מתאפסת כאשר \( 2t^{2}=t \), כלומר ב-\( t=0 \) (שלא יכול לקרות, כזכור) או ב-\( t=\frac{1}{2} \), כלומר \( 3^{x}=\frac{1}{2} \), כלומר ב-\( x=\log_{3}\frac{1}{2} \). זה לא כל כך מעניין מה המספר המדויק הזה פרט לכך שהוא שלילי. בנקודה הזו יקרה לגרף הפונקציה דבר מוזר - היא תעבור מקמירות לקעירות. זה משהו הכרחי- כי השאיפה של הפונקציה לאסימפטוטה כשאיקס שואף למינוס אינסוף מכריח אותה להיות קעורה, בזמן שהשאיפה של הפונקציה לאינסוף כשאיקס שואף לאינסוף מכריחה אותה להיות קמורה. כך שמעבר מקעירות לקמירות חייב להתקיים. הנקודה שמעניינת אותי הוא שהמעבר הזה לא מתקיים ב-\( x=0 \) אלא לפניו.

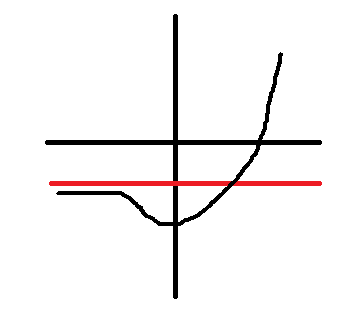
נשאר לצייר סקיצה. בסקיצה אני מתחשב בדברים הבאים: א) נקודת המינימום ב) האסימפטוטה ג) נקודת החיתוך עם ציר \( y \) ב-\( x=1 \) ד) כל הדיון שניהלתי למעלה על קמירות וקעירות. הנה הסקיצה:

סעיף ב'

הייתה לי טעות מטופשת במיוחד בסעיף הזה - חישבתי בהתחלה את השטח הלא נכון. במקום לחשב את השטח שמוגבל על ידי גרף הפונקציה מתחת לאסימפטוטה, חישבתי את זה שמעל האסימפטוטה. זו אשמתי המלאה - קריאה לא נכונה של התיאור שלהם את השטח שאמורים לחשב. זו כבר טעות מפגרת שניה שלי במבחן. האם זה אומר שאני פותר אותו בשעות מאוחרות מדי? האם בזמן אמת הייתי עושה את אותן טעויות? לא יודע.

בואו נפתור את השאלה הנכונה. מה שאנחנו רוצים הוא לחשב את מינוס האינטגרל מ-\( x=0 \) ועד ל-\( x \) שהוא נקודת החיתוך של הפונקציה עם האסימפטוטה (הקו האדום אצלי). אם כן, צריך להתחיל מלשאול את עצמנו מהי נקודת החיתוך הזו. כלומר מתי \( f\left(x\right)=-3 \), כלומר מתי \( \left(3^{x}\right)^{2}-2\cdot3^{x}-3=-3 \), כלומר מתי \( t^{2}=2t \). כרגיל, \( t=0 \) נפסל ולכן נקבל \( t=2 \), כלומר \( 3^{x}=2 \), כלומר \( x=\log_{3}2 \). בנקודה הזו \( 9^{x}=4 \) ואילו \( 3^{x}=2 \) וזה אכן מסתדר.

עכשיו, שימו לב שהאינטגרל הזה ייתן לי יותר מדי שטח, כי האינטגרל מודד את השטח שכלוא בין גרף הפונקציה לבין ציר \( x \). כאן אני צריך למדוד את השטח שכלוא בין גרף הפונקציה ובין האסימפטוטה. יש שתי דרכים לעשות זאת: אפשר לחשב את האינטגרל הרגיל ואז להחסיר את שטח המלבן שספרתי “בטעות”, ואפשר פשוט “להרים” את הפונקציה על ידי כך שאחשב את האינטגרל של \( f\left(x\right)+3=9^{x}-2\cdot3^{x} \), חישוב שיהיה לי יותר פשוט. תדמיינו שאני לוקח את גרף הפונקציה כולה ודוחף אותו למעלה, יחד עם קו האסימפטוטה והכל, כדי להבין למה זה יעבוד.

אם כן, האינטגרל שלי הוא:

\( \int_{0}^{\log_{3}2}\left(9^{x}-2\cdot3^{x}\right)dx=\left[\frac{9^{x}}{\ln9}-\frac{2\cdot3^{x}}{\ln3}\right]_{0}^{\log_{3}2}= \)

\( =\left(\frac{4}{2\ln3}-\frac{2\cdot2}{\ln3}\right)-\left(\frac{1}{2\ln3}-\frac{2}{\ln3}\right) \)

\( =\left(-\frac{4}{2\ln3}\right)-\left(-\frac{3}{2\ln3}\right) \)

\( =-\frac{1}{2\ln3} \)

ולכן הפתרון, שהוא כאמור מינוס האינטגרל הזה, הוא \( \frac{1}{2\ln3} \)

סעיף ג'

כאן עושים התחכמות ומרימים את \( f \) עוד קצת. מה שצריך להבין פה הוא שכשמרימים את הפונקציה \( f \) זה לא משנה את השטח שכלוא בינה, בין ציר \( y \) ובין הקו הישר של האסימפטוטה, אחרי שאנחנו מרימים גם את הקו הישר הזה. מה שעשיתי בסעיף הקודם היה להרים את הקו של האסימפטוטה כך שינוח על ציר \( x \); בסעיף הזה הם מרימים אותו עוד קצת, כך שהוא הופך להיות הישר \( y=1 \). השטח לא משתנה כתוצאה מכך, ולכן הערך של \( k \) הוא \( 1 \).

מה דעתי על השאלה?

זו שאלת חדו”א סטנדרטית. כאמור, לא ברור לי מה ההבדל המהותי בינה לבין שאלות החדו”א בחלק א’ של המבחן, ואני לא מבין למה צריך כל כך הרבה חדו”א. אז בחלק א’ הפונקציות היו טריגונומטריות וכאן הן אקספוננטים. למי אכפת?

שאלה 5

השאלה הזו מזכירה לי במבט ראשון את השאלה ההיא מחלק א’ שאהבתי. בואו נקווה שזה לא יתגלה בתור דמיון שטחי נטו.

סעיף א'

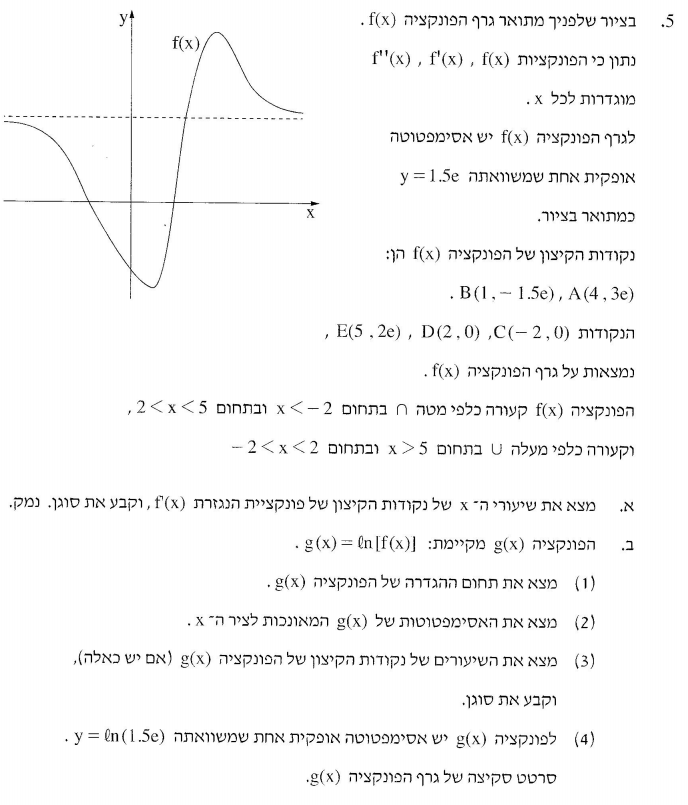
טוב, יש המון מה לקרוא ועד שאני מסיים אני כבר לא זוכר כלום, אבל אני מאוד מתרשם לטובה מכך שבמקום לומר “קעורה” ו”קמורה” הם אומרים “קעורה כלפי מטה” ומוסיפים \( \cap \) ו”קעורה כלפי מעלה” ומוסיפים \( \cup \). ככה באמת קשה להתבלבל (הטרמינולוגיה שאני מכיר היא לומר “קעורה” בשביל “קעורה כלפי מטה” ו”קמורה” בשביל “קעורה כלפי מעלה”; אני זוכר את זה כי אני זוכר ש”קעורה” אמור להיות כמו קערה, רק הפוך. אני בעיקר זוכר את ה”הפוך” הזה כי הוא מרגיז נורא).

מה שמבקשים ממני הוא למצוא את שיעורי ה-\( x \) של נקודות הקיצון של הנגזרת של \( f \) (כי את נקודות הקיצון של \( f \) נתנו לי במפורש). נקודת קיצון של \( f^{\prime} \) היא נקודה שבה הפונקציה מפסיקה להיות עולה ומתחילה להיות יורדת, או ההפך. זה בא לידי ביטוי בגרף של \( f \) במעבר מקמירות לקעירות: אם \( f^{\prime} \) היא פונקציה עולה בתחום מסויים, אז \( f \) היא קמורה באותו התחום, ואילו אם \( f^{\prime} \) היא יורדת אז \( f \) היא קעורה.

נקודות המעבר בין קמירות לקעירות הן בדיוק \( x=-2 \), \( x=2 \) ו-\( x=5 \). ב-\( x=-2 \) וב-\( x=5 \) הפונקציה עוברת מקעירות לקמירות, ולכן אלו נקודות שבהן \( f^{\prime} \) עוברת מירידה לעלייה, כלומר אלו נקודות מינימום, ואילו ב-\( x=2 \) הפונקציה עוברת מקמירות לקעירות ולכן זו נקודת מקסימום של \( f^{\prime} \).

סעיף ב'

מכיוון ש-\( \ln\left(x\right) \) מוגדרת רק עבור \( x>0 \) מקבלים שתחום ההגדרה של \( g\left(x\right)=\ln\left(f\left(x\right)\right) \) הוא \( x<-2 \) ו-\( x>2 \). ומתי תהיה אסימפטוטה אנכית? אסימפטוטה אנכית פירושה שהפונקציה שואפת לאינסוף או למינוס אינסוף כאשר \( x \) שואף לנקודה (ולא לאינסוף). כאן זה יקרה בדיוק עבור \( x=-2 \) ועבור \( x=2 \) (בשניהם השאיפה היא למינוס אינסוף כי \( f\left(x\right) \) שואפת לאפס בנקודות הללו).

נותר לדבר על נקודות קיצון. מכיוון ש-\( \ln x \) היא פונקציה מונוטונית עולה, הרי ש-\( \ln\left(f\left(x\right)\right) \) תחלוק את אותן נקודות קיצון עם \( f\left(x\right) \). בתחום ההגדרה של \( g\left(x\right) \) נמצאת רק נקודת הקיצון של \( x=4 \), שבה מתקיים \( f\left(4\right)=3e \) ולכן \( g\left(4\right)=\ln\left(3e\right)=1+\ln3 \). זוהי נקודת מקסימום עבור \( f\left(x\right) \) ולכן גם עבור \( g\left(x\right) \) זוהי נקודת מקסימום.

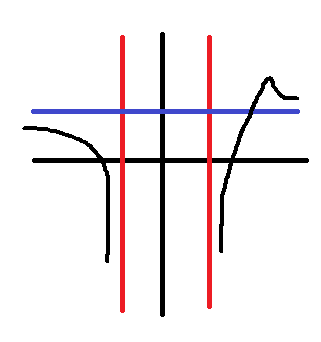
לסיום, נותר לצייר את הגרף של \( g \). אומרים לנו משהו על האסימפטוטה האופקית שלה וזה נראה לי מיותר כי את כל זה אפשר לדעת ממה שאמרו לנו על האסימפטוטה האופקית של \( f \).

בשרטוט אני מתחשב בדברים הבאים: א) תחום ההגדרה ב) האסימפטוטות האנכיות שמצאתי ג) האסימפטוטה האופקית המדוברת ד) נקודת המקסימום ב-\( x=4 \) ה) העובדה שהפונקציה עולה ויורדת כמו \( f \).

מה דעתי על השאלה?

שוב, שאלת חדו”א סטנדרטית. דומה לזו של חלק א’. נחמדה. לא משהו מיוחד.

אז מה למדנו מכל זה?

תמה ונשלמה הבגרות. ראשית, איך הלך לי? יחסית סביר, בהתחשב בכך שלא התכוננתי למבחן, ובכך שלא פתרתי בתנאי מבחן כך שהריכוז שלי היה נמוך ודילגתי מעל שלבים וכדומה. אלו התירוצים שמצדיקים את העובדה שהמון דברים לא זכרתי, והיו לי גם שגיאות מזעזעות. יש כמה שאלות שפתרתי על סמך הידע הקיים שלי למרות שכנראה בבית הספר לומדים דרכים אחרות להתמודד איתם, אבל בהרבה מקרים לא הרגשתי שהידע שלי מסייע במיוחד. אין גם ספק בכך שכמעט כל השאלות היו “לא כיפיות” - לא הזכירו לי את הדברים שאותי אישית מעניינים במתמטיקה. זו לא בדיוק ביקורת על הבגרות כי אני חושב שבגרות על מה שמעניין אותי הייתה מסתיימת באסון עבור התלמידים.

ייתכן שאתם מצפים לאיזה סיכום מעמיק שבו אשטח את התובנות שלי על שיטת הלימוד בבתי הספר וכיצד יש לשנותה מן היסוד. אבל אני בוודאי לא אעשה שום דבר מוזר שכזה. אני מעדיף להסתכל על הדברים החיוביים פה, ויש כמה: ראשית, המבחן הרגיש לי הוגן בהחלט - לא שאלות שמטרתן להכשיל או להקשות בכוונה. הרוב היה סטנדרטי ודורש בעיקר היכרות טובה עם החומר ושליטה בו - שזה מה שאמור לקרות בבגרות. שנית, לא מעט שאלות נראו לי עוסקות בנושאים חשובים, כאלו שלא הייתי מוותר עליהם. עיקר התמיהה שלי מופנה לכיוון חדו”א, שאני מרגיש שיש הרבה יותר מדי ממנו במבחן.

דבר אחד שאיני יודע כלל, כי לא בדקתי זאת, הוא מה ההבדלים בין המבחנים הללו ובין המבחנים של תלמידי 3 ו-4 יחידות. על פניו אני לא מרגיש שהיה במבחן הזה משהו “מיוחד” ולכן לא בטוח שאני מבין את כל הקמפיינים של השנה שעברה שמטרתם לעודד 5 יחידות לימוד במתמטיקה בתור סוג של כרטיס כניסה לחיים ליקום ובכלל. אני רוצה לנצל את סיום הפוסט הזה כדי להפנות מסר פשוט לתלמידים, בתור מישהו שיש לו קצת נסיון עם מתמטיקה ואוהב אותה: מתמטיקה תיכונית היא לא סוף הסיפור וגם לא עיקר הסיפור. גם אם אתם עושים עכשיו 3 או 4 יחידות. גם אם אתם לא מבינים את החומר. גם אם המתמטיקה שאתם לומדים משעממת או מעצבנת אתכם, אל תראו בזה סוף הסיפור. אל תתנו לזה לסגור לכם את הדלת בפרצוף. אל תתנו לזה לגרום לכם לוותר על דברים בעתיד באופן אוטומטי. מתמטיקה אוניברסיטאית (גם כזו שנלמדת בפני עצמה וגם כזו שנלמדת על מנת לשמש את הסטודנטים בתחומים אחרים) היא אמנם קשה ותובענית, אבל היא גם מתגמלת יותר, וגם אופי הקשיים בה הוא שונה מהותית. אני לא מציע לכולכם לרוץ ללמוד מתמטיקה או אפילו להתעניין בה, אבל אם אתם מגיעים להחלטה בעניין, אני מקווה שהחוויות שלכם מהתיכון לא יהיו הגורם המכריע.